Multilevel Modeing (with R) Part 1

Princeton University

Jason Geller, PH.D.(he/him)

2024-01-31

Overview

  • The nuts and bolts of multilevel models

    • Why do we need multilevel models? what are they? and why are they awesome?
    • Important terminology
    • How we specify MLMs (in code and mathematically)

  • How to do it (Monday)

    • Organizing data for MLM analysis
    • Estimation
    • Fit and interpret multilevel models
    • Effect size
    • Power
    • Visualizing data
    • Reporting

Packages

  • Packages you will need
library(tidyverse)
library(easystats)
library(here)
library(knitr)
library(broom.mixed)
library(lme4)

Why multilevel modeling?

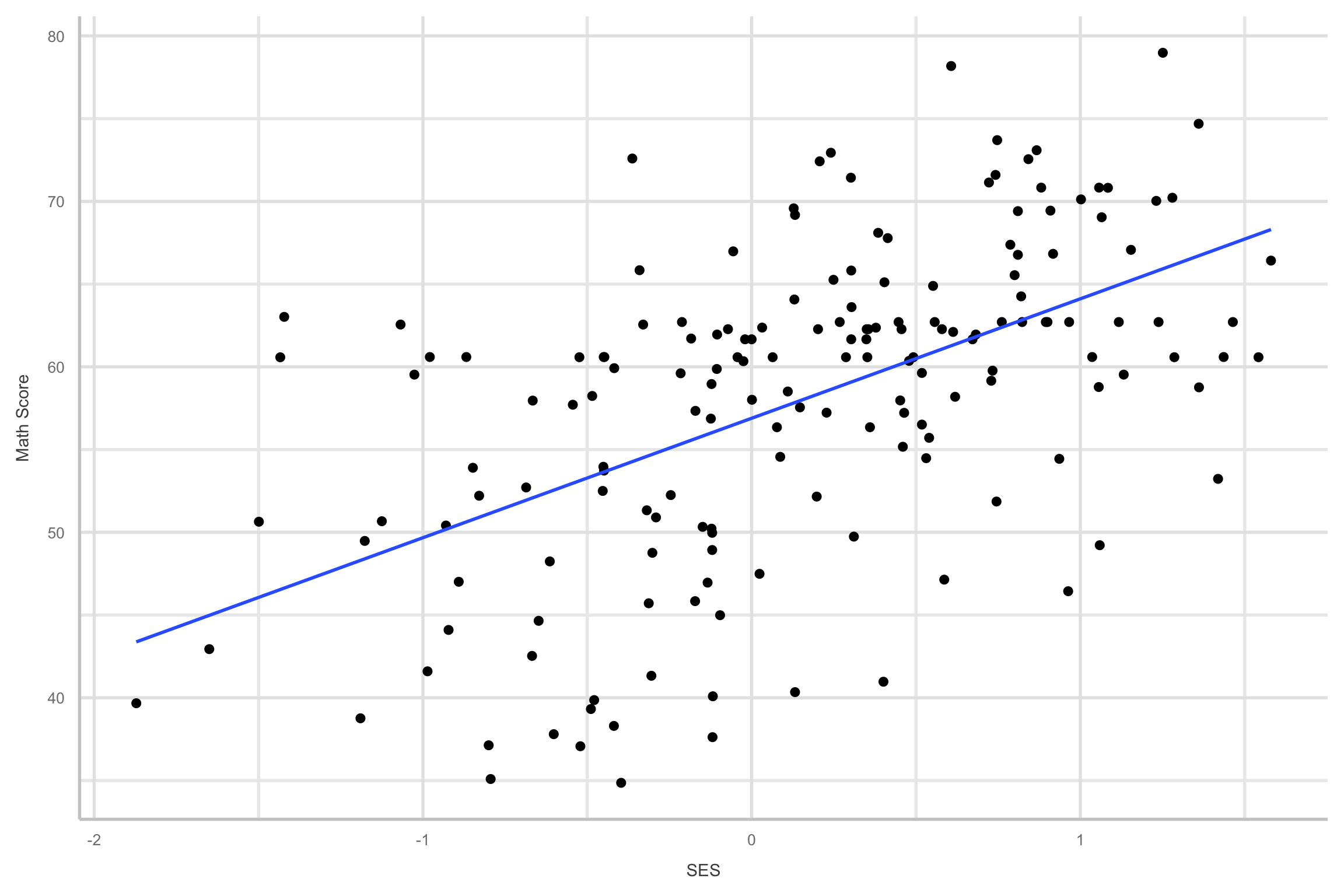
  • Let’s look at the relationship between SES and math achievement
data <- read.csv("https://raw.githubusercontent.com/jgeller112/PSY504-Advanced-Stats-S24/main/slides/02-MLM/data/heck2011.csv")

lm(math~ses, data=data) %>%
tidy() %>%
  kable()
term estimate std.error statistic p.value
(Intercept) 57.598169 0.0981885 586.60833 0
ses 4.254676 0.1256614 33.85826 0

Why multilevel modeling?

  • However, if we introduce grouping we tell a slightly different story

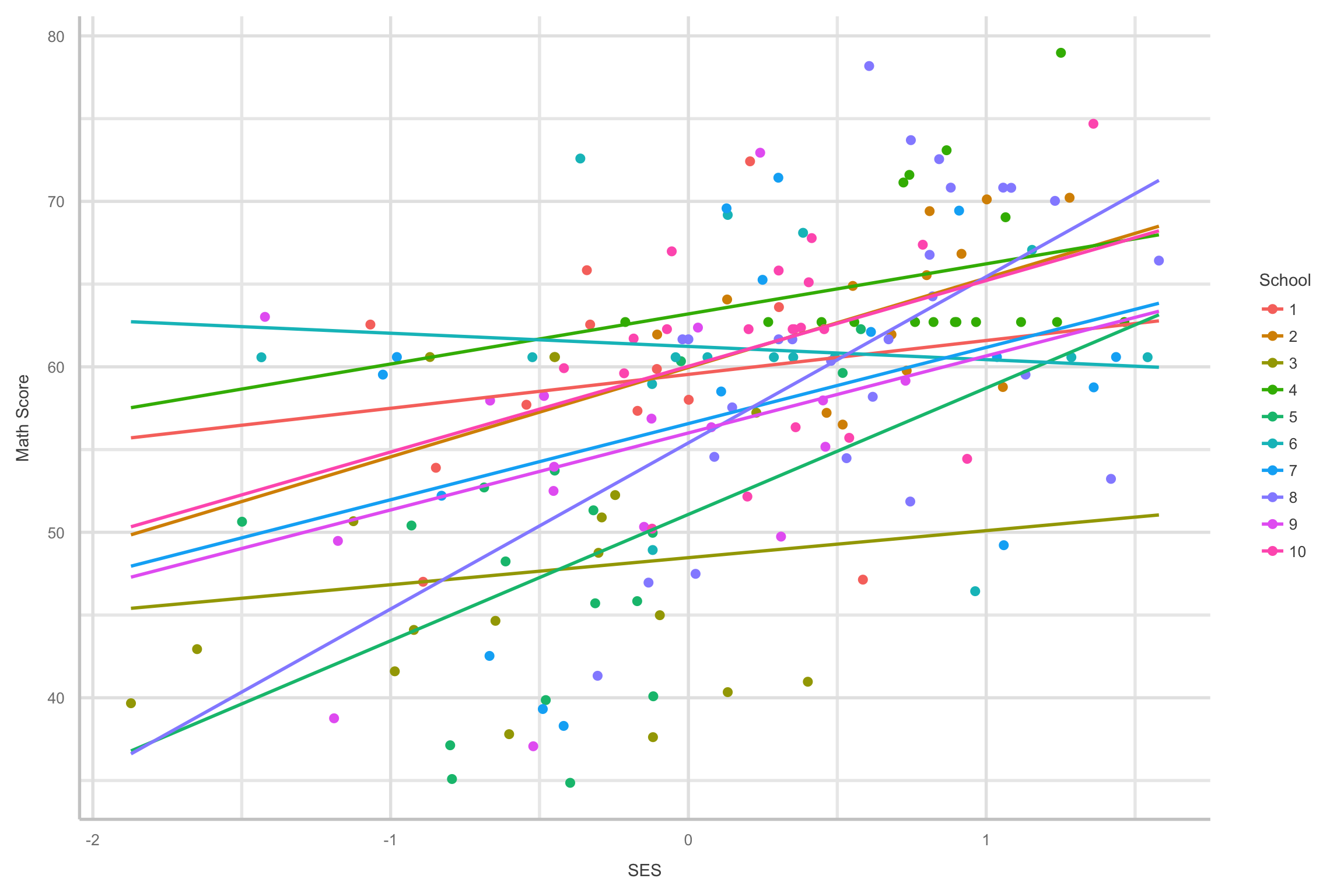
Why multilevel modeling?

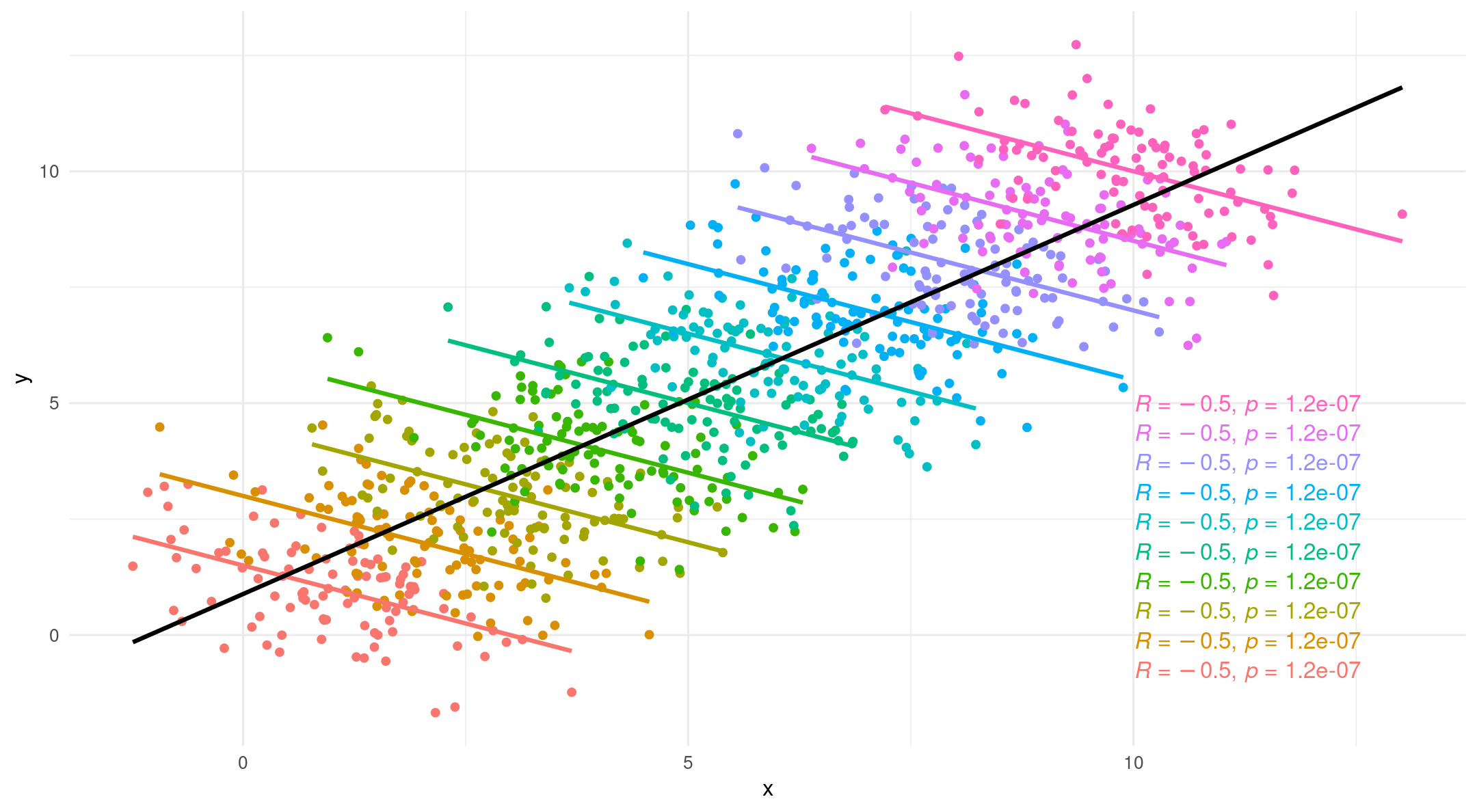
  • Simpson’s paradox

  • A phenomenon in which a trend appears in several groups of data but disappears or reverses when the groups are combined

Why multilevel modeling?

  • The word we live in is highly interdependent!

    • Biological, psychological, social processes occur at multiple levels

Why multilevel modeling?

What is multilevel modeling?

Chelsea Parlett-Pelleriti

  • An elaboration on regression

    • just extra errors!

What is multilevel modeling?

  • Technique that allows us deal with non-independence between data points (i.e., clustered/nested data)

    • Nested data violate key assumptions of OLS
      • independent observations
      • independent errors
        • Underestimates SE and increases Type 1 error
    • Correct inferences!

  • Explicit partitioning of the variance

    • Within (intra-group differences)

    • Between (inter-group differences)

What is a “hierarchy?”

Clustering = Nesting = Grouping = Hierarchies

  • Key idea: More than one dimension sampling simultaneously

    • “Nested” designs

    • Repeated-measures and longitudinal designs

    • Any complex mixed design

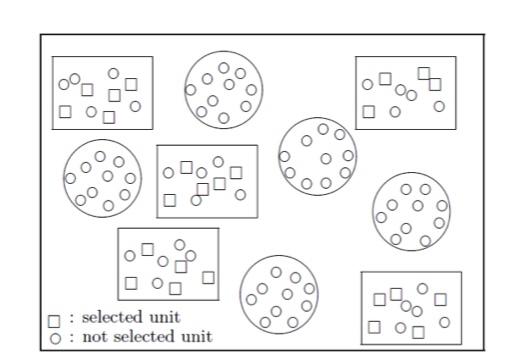
Nested designs

Two-level Hierarchy

  • Nested designs

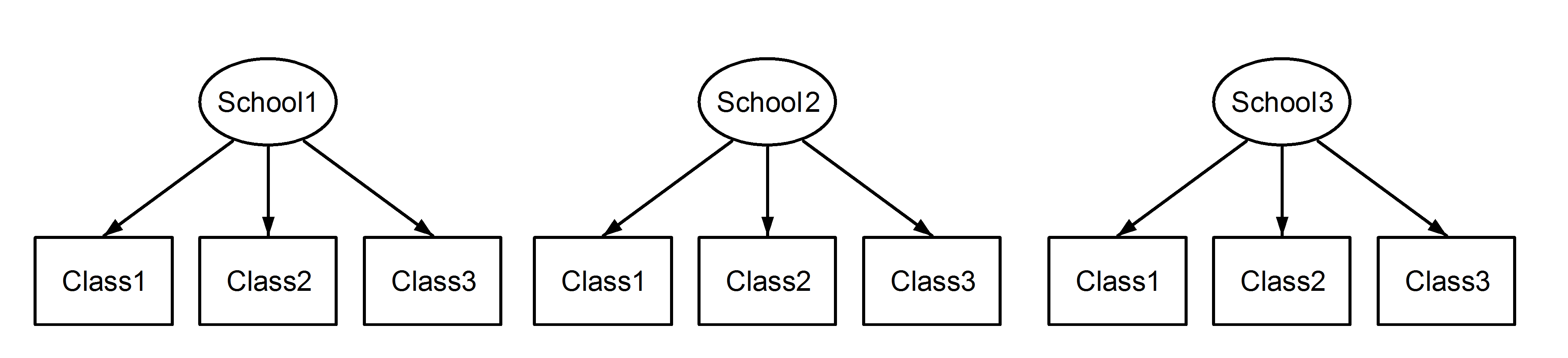
  • For now we will focus on data with two levels:

    • Level one: most basic level of observation
    • Level two: groups formed from aggregated level-one observation

Three-level Hierarchy

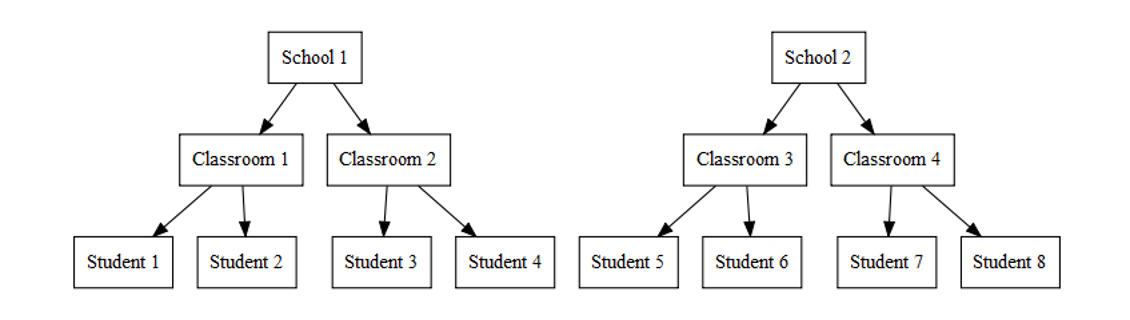
Crossed vs. nested designs

  • Crossed designs (sometimes called cross-classified)

    • When lower units do not belong to only one higher level unit

Repeated designs

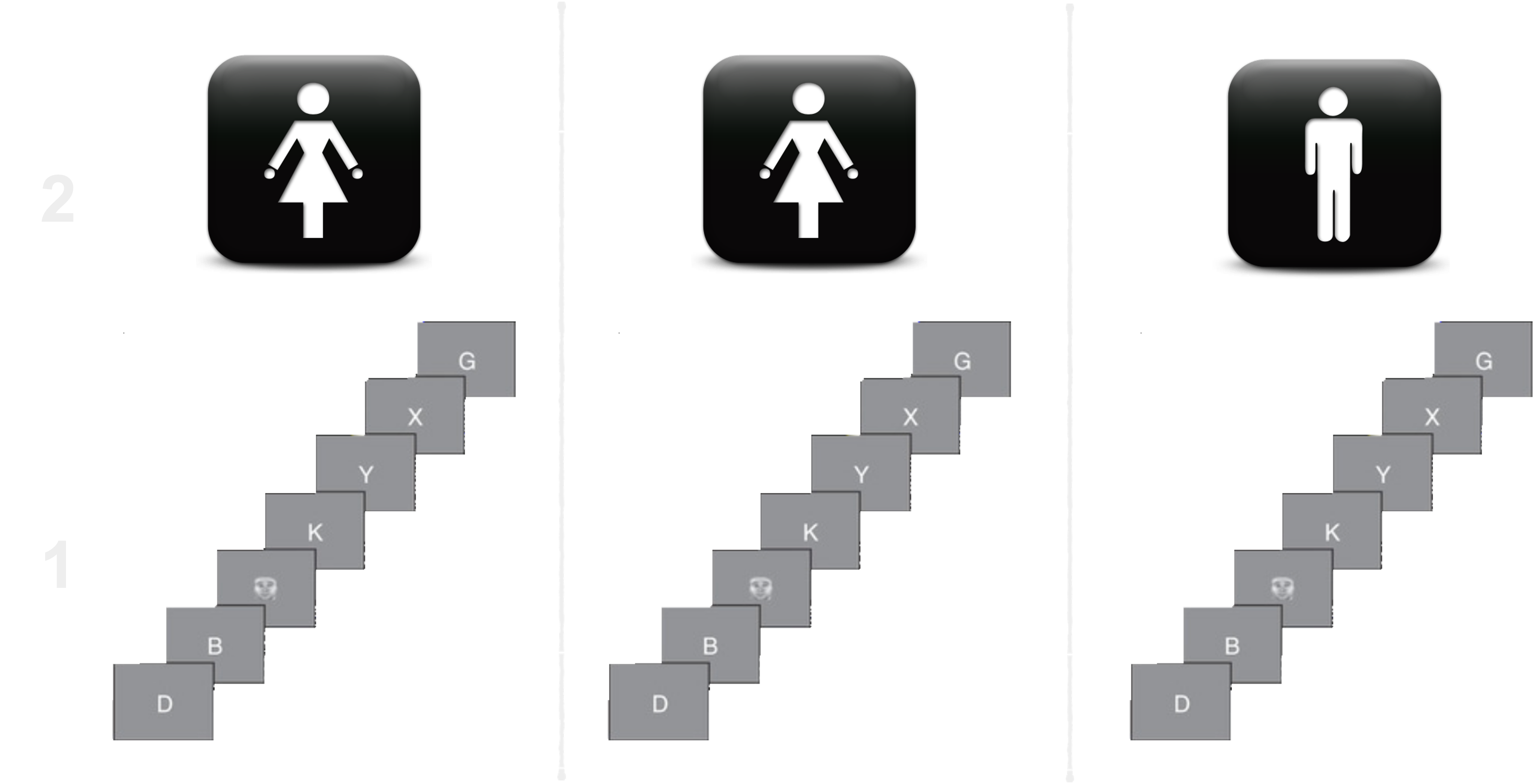
Repeated designs

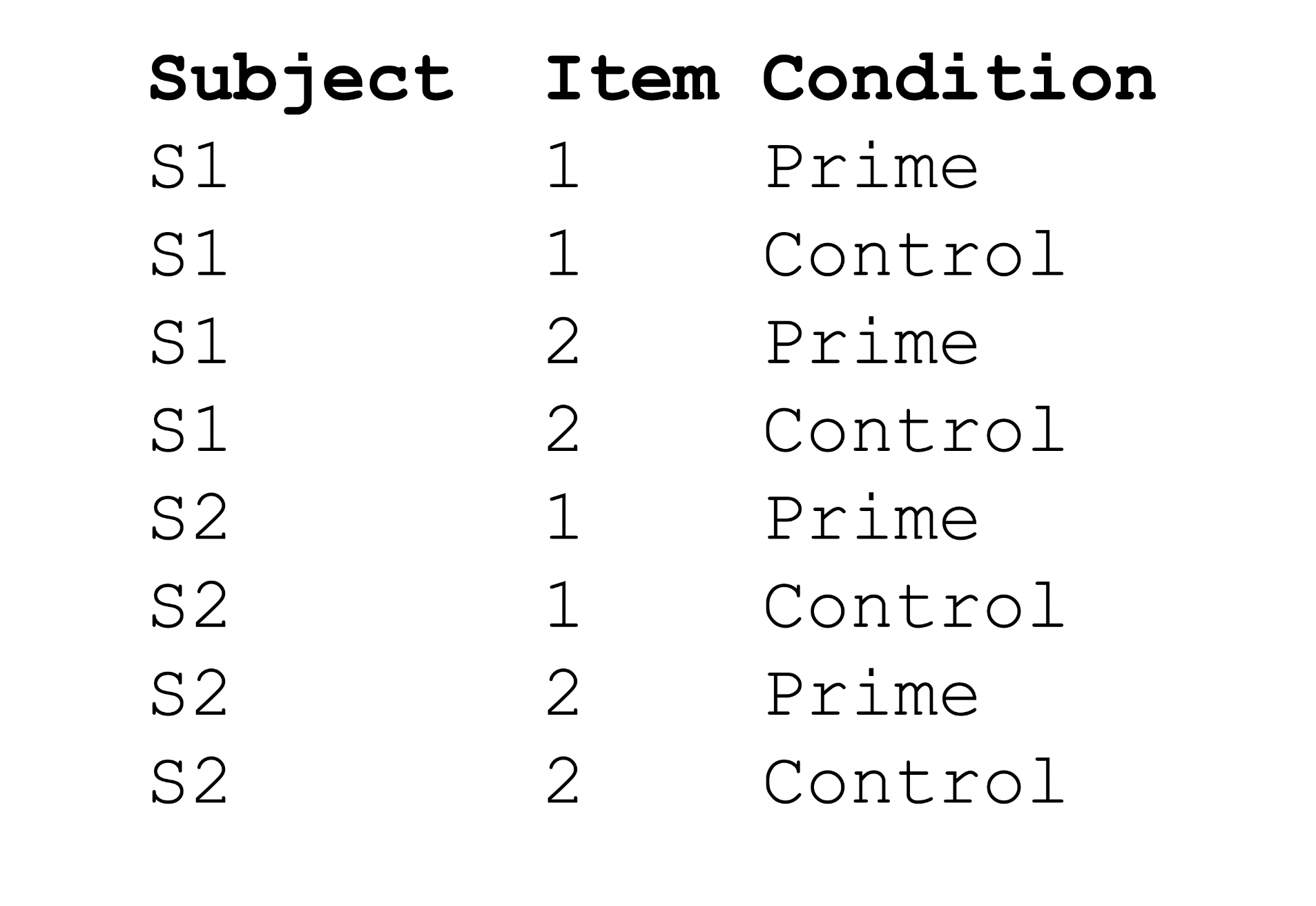
Repeated designs

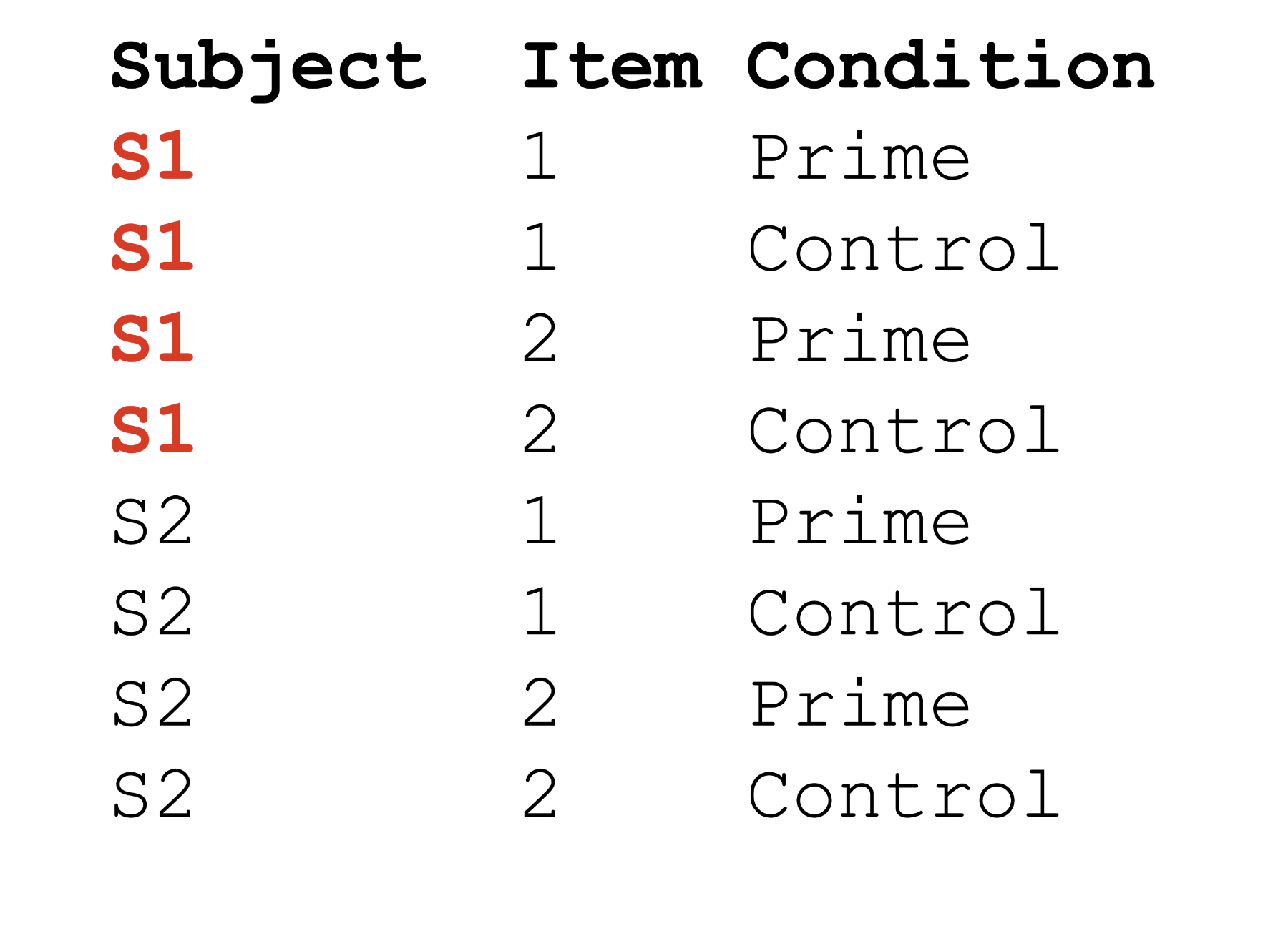
Repeated designs

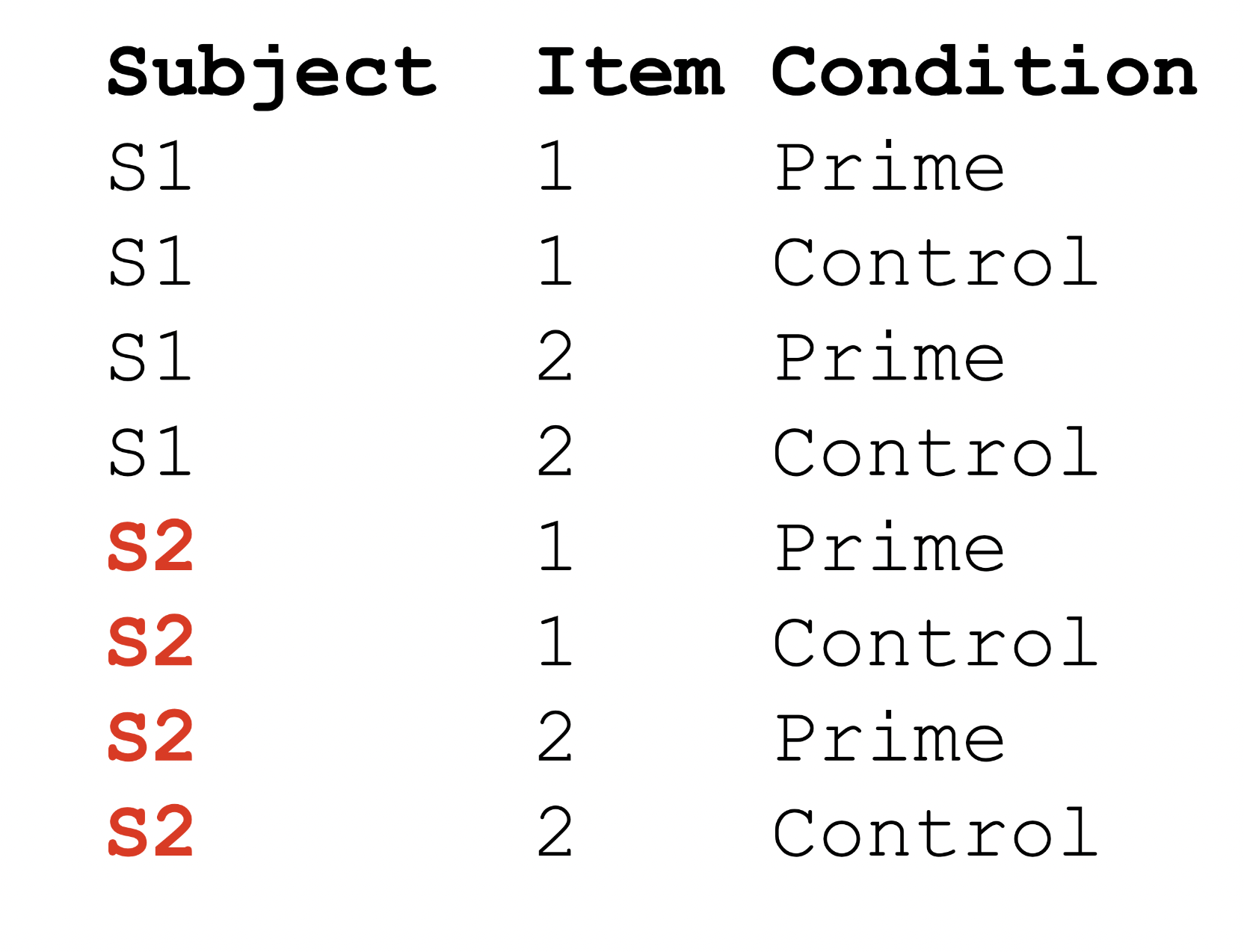
Repeated designs

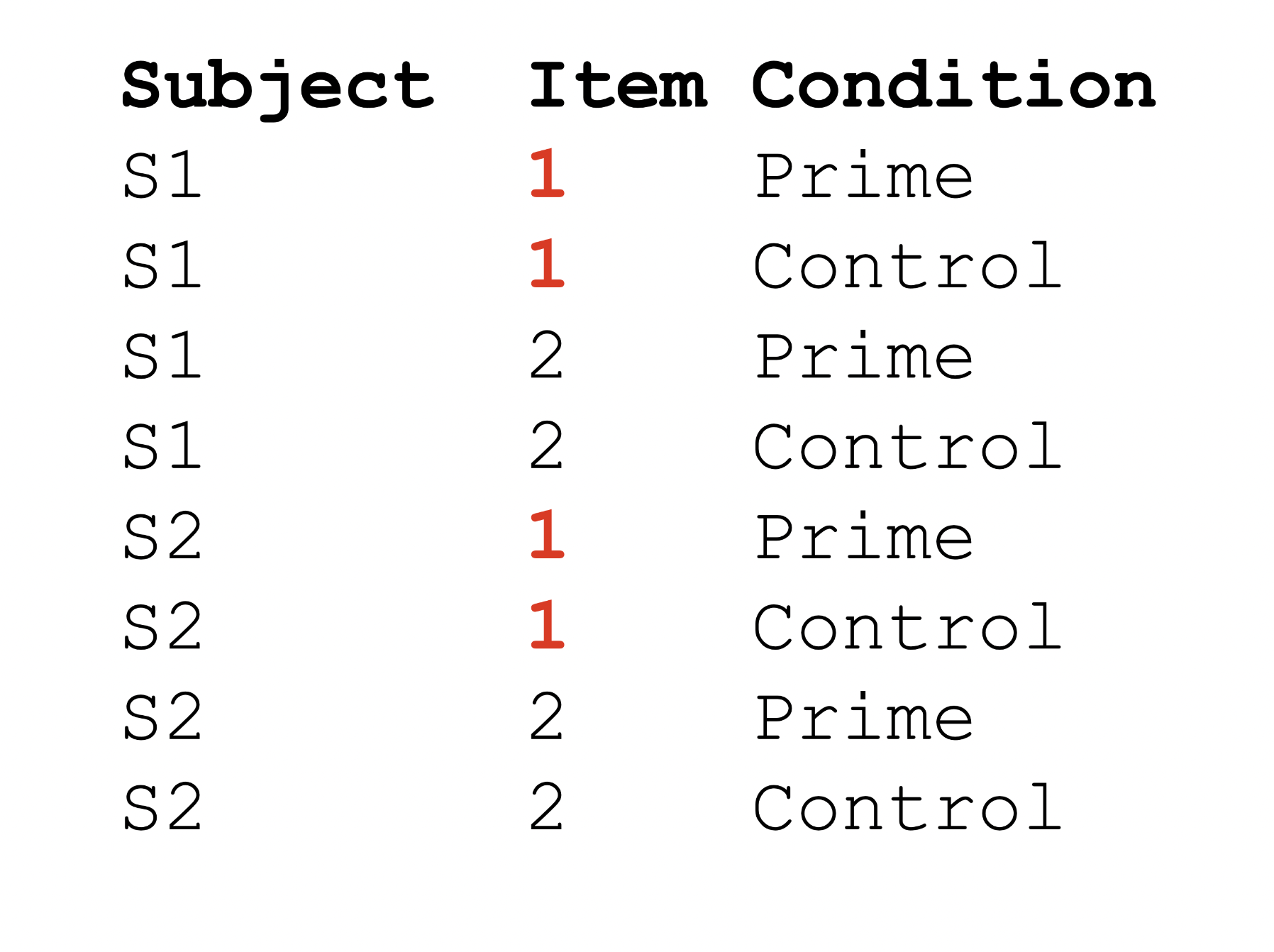
Repeated designs

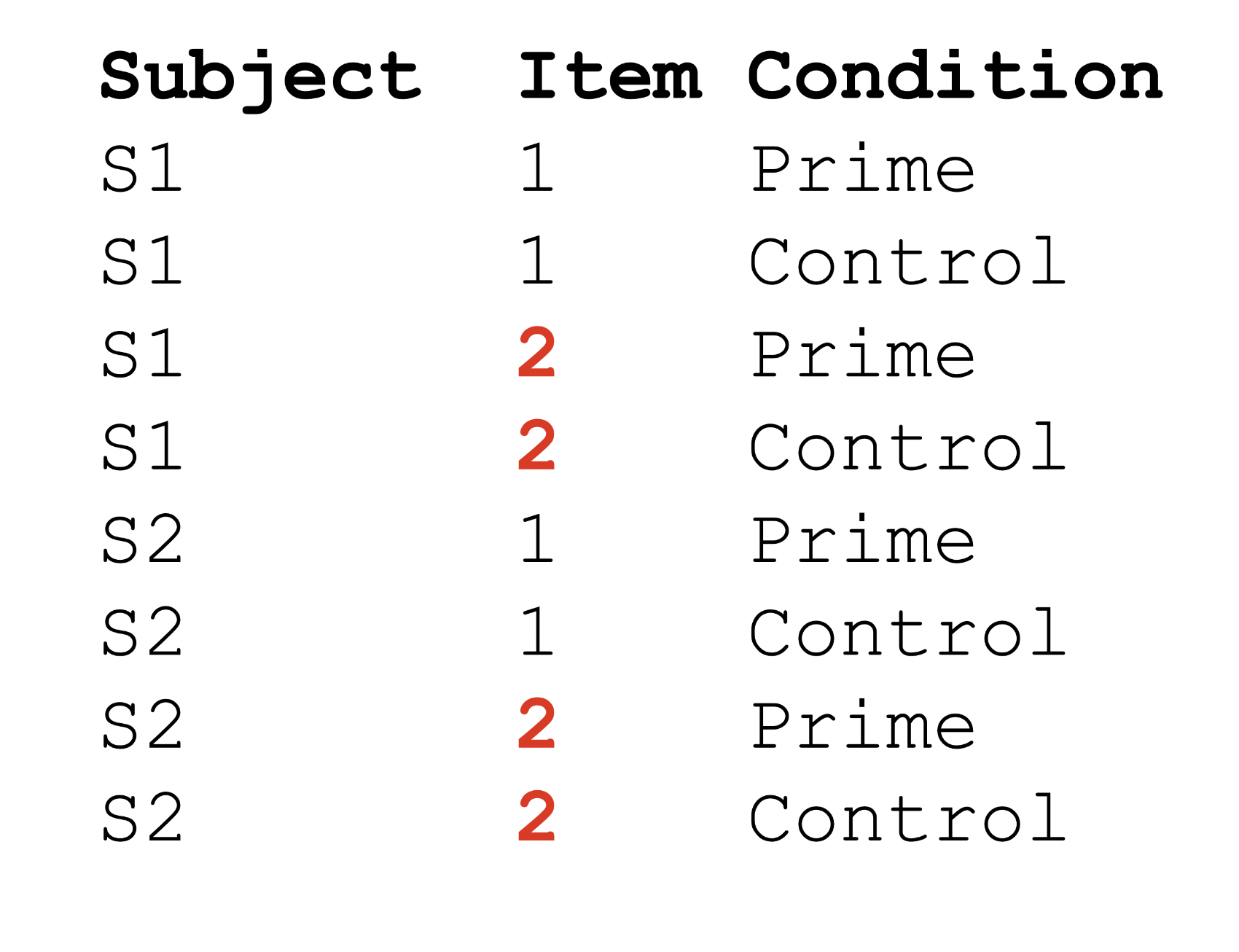
Longitudinal designs

Test your knowledge

Radon is a carcinogen – a naturally occurring radioactive gas whose decay products are also radioactive – known to cause lung cancer in high concentrations. The EPA sampled more than 80,000 homes across the U.S. Each house came from a randomly selected county and measurements were made on each level of each home. Uranium measurements at the county level were included to improve the radon estimates.

  1. What is the most basic level of observation (Level One)?
  2. What are the group units (Level Two, Level Three, etc…)?

Multilevel models are awesome!

Why MLM is Awesome

  • Classic analysis:

    • Aggregate to level of the group (e.g., with means)

  • Drawback of classic analysis:

    • Loss of resolution!
    • Loss of power!

  • MLM Approach:

    • Deaggregation (keep all the data)

Why MLM is Awesome

  • Classic Analysis:

    • Repeated-measures ANOVA

  • Drawback of this approach:

    • Missing data

      • Must exclude entire people OR, you can interpolate missing data

  • MLM Approach:

    • Can analyze all the observations you have!

Why MLM is Awesome

  • Classic Analysis:

    • Repeated-measures ANOVA

  • Drawback of ANOVA:

    • Only use categorical predictors

  • MLM Approach:

    • Can use any combo of categorical and continuous predictors!

Why MLM is Awesome

  • Interdependence
    • You can model the relationships between cases (regression for repeated observations)
  • Missing data
    • Uses ML for missing data
  • Power
    • Deaggregated data
  • Take into account within and between variance
  • Flexibility

Multilevel models

  • When to use them:

    • Nested designs

    • Repeated measures

    • Longitudinal data

    • Complex designs

  • Why use them:

    • Captures variance occurring between groups and within groups

  • What they are:

    • Linear model with extra residuals

Why not use MLM?

  • Dont really care about variance (it is just a nuisance variable)

    • Use GEEs (generalized estimating equations)
    • Clustered standard errors

  • Data is not actually interdependent

    • Test with ICC (Monday)

  • Small number of groups/clusters

  • You only have a between-subjects design

Important Terminology

Jumping right in

  • Words you hear constantly in MLM Land:

    • Fixed effects
    • Random effects
    • Random factors
    • Random intercepts
    • Random slopes

  • What do they all mean?

Fixed and random effects

  • Two sides to any model

    \[ y_i = \color{blue}{b_{0_{\text{(intercept)}}} + b_{1_{\text{(slope)}}} x_i} + e_{i_{\text{(error)}}} \]

    • Model for the means (fixed part):

      • Fixed effect (constant effect):

        • Population-level (i.e., average) effects that should persist across clusters/experiments

Note

  • What you are used to caring about for testing hypotheses
  • Our predictor variables (can be continuous or categorical)

Fixed and random effects

  • Model for the variance (random part):

\[ y_i = {b_{0_{\text{(intercept)}}} + b_{1_{\text{(slope)}}} x_i} + \color{red}{e_{i_{\text{(error)}}}} \]

  • Uncorrelated with fixed part

  • Variation around the expected values

  • Normal distributed ~ \(N(\mu,\sigma)\)

  • In MLM multiple “piles of variance” or residual terms

Random factors and random effects

  • Random factors:

    • Represent higher level grouping variables

      • A random sample of an infinite number of possible levels

  • Note

    Can only be categorical!

Random factors vs random effects

  • The random factor is your clustering variable:

    • Participants 🧑‍🤝‍🧑

    • Schools 🏫

    • Words

    • Pictures 🖼️

Random factors vs random effects

  • Random effects:

    • How random factors are allowed to vary

      • Random intercept (most common) : \(U_{0j}\)

        • Each level-2 cluster has its own average level-1 outcome

      • Random slope: \(U_{1j}\)

        • Each level-2 cluster has its own coef for the effect of a predictor on the outcome

          • You have a choice about whether or not to allow your Level 1 intercept and slopes to have variability

Is it a random or fixed factor?

  • Should my variable be fixed or random?

    • If it is continuous, has few levels (<5), or is an experimental manipulation

      • Fixed

  • Want to estimate variance at each level of factor?

    • Fixed

  • Want a general estimate of variance of factor?

    • Random

What is random and what is fixed?

  • Scenario: Investigating how student performance is influenced by teaching methods and individual student characteristics across different schools.

    • Data Collected: student socio-economic status (SES), teaching method used (e.g., traditional, modern), and school ID

      • What is fixed?

      • What is random?

Specifiying MLMs

Single-level (fixed) regression

  • Blue = fixed

  • Red = random

    \[y_i = \color{blue}{b_{0_{\text{(intercept)}}} + b_{1_{\text{(slope)}}} x_i} + \color{red}{ e_{i_{\text{(error)}}}}\]

\[ e_{i_{\text{(error)}}} = y_i - \hat{y}_i \]

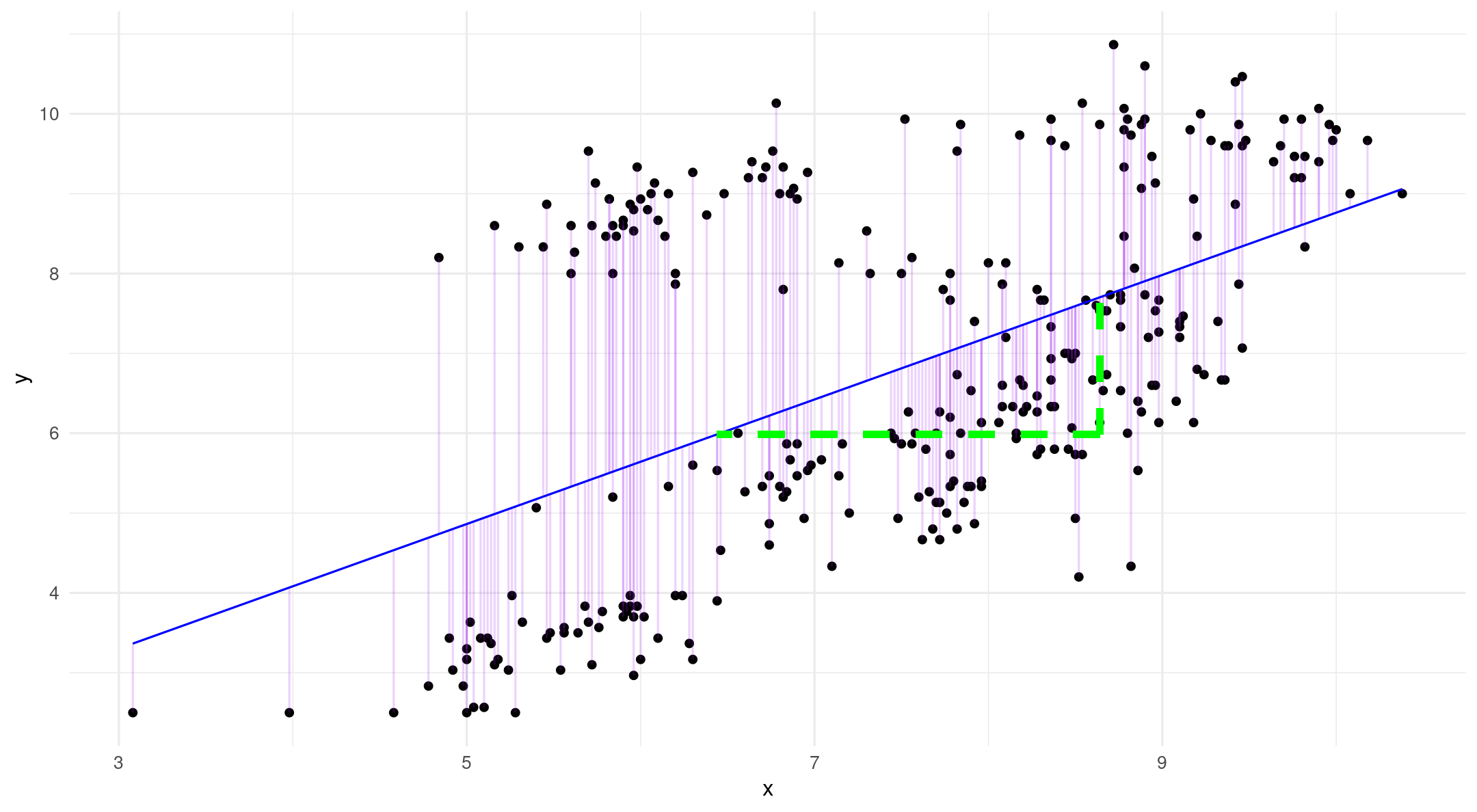
Random intercept

  • Varying starting point per higher level/group variable

\[ y_{ij} = (\color{blue}{b_{0j_{\text{(intercept)}}}} + \color{red}{U_{0j_{\text{(random intercept)}}}}) + \color{blue}{b_{1_{\text{(slope)}}} x_{ij}} + \color{red}{e_{ij_{\text{(error)}}}} \]

\[ U_{0j} = b_{0j} - b_0 \]

  • Between-group variation

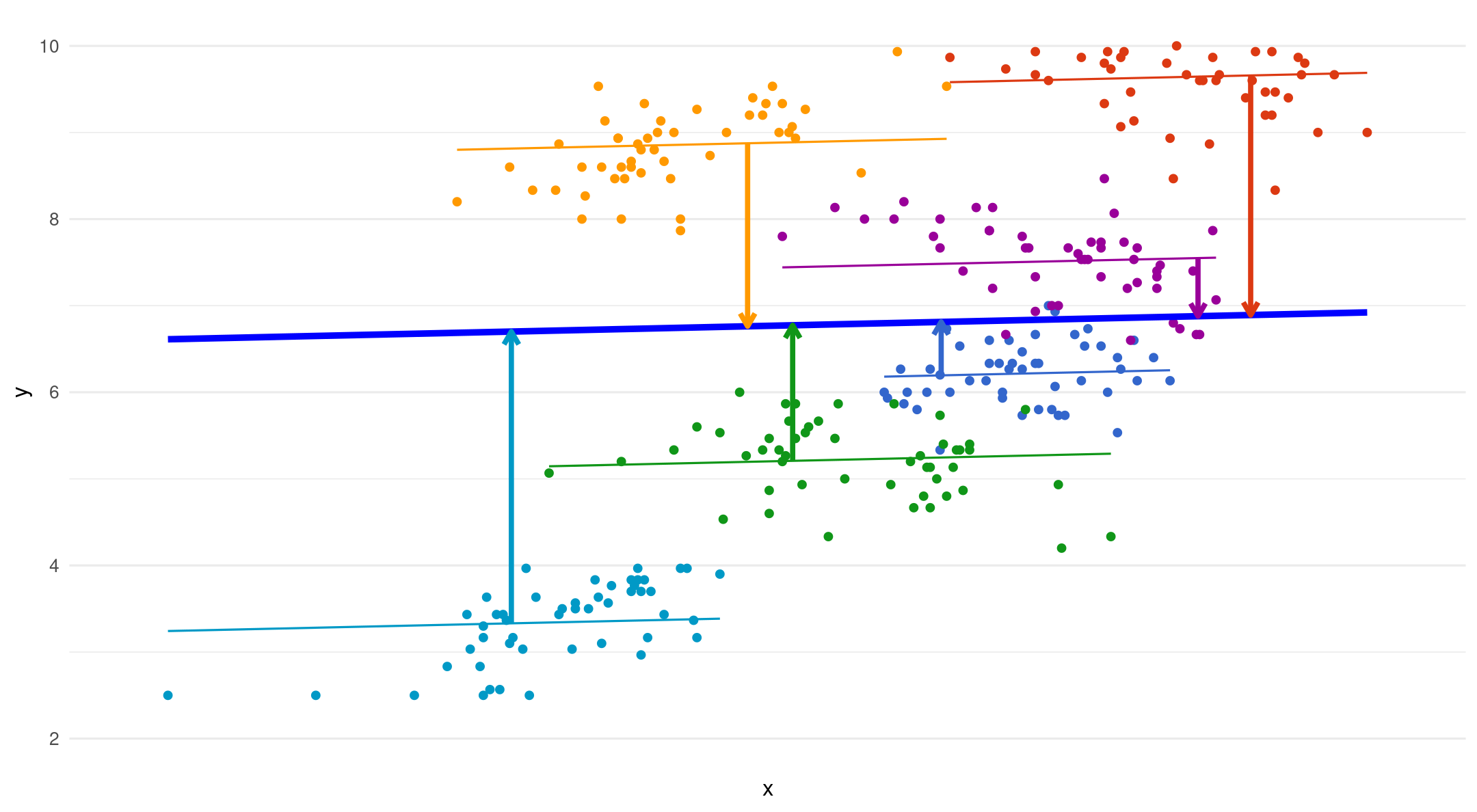
i = individual observation j = group

Random intercepts

\[ y_{ij} = ({b_{0j_{\text{(intercept)}}} + U_{0j_{\text{(random intercept)}}}}) + b_{1_{\text{(slope)}}} x_{ij} + \color{red}{ e_{ij_{\text{(error)}}}} \]

Within-group variation

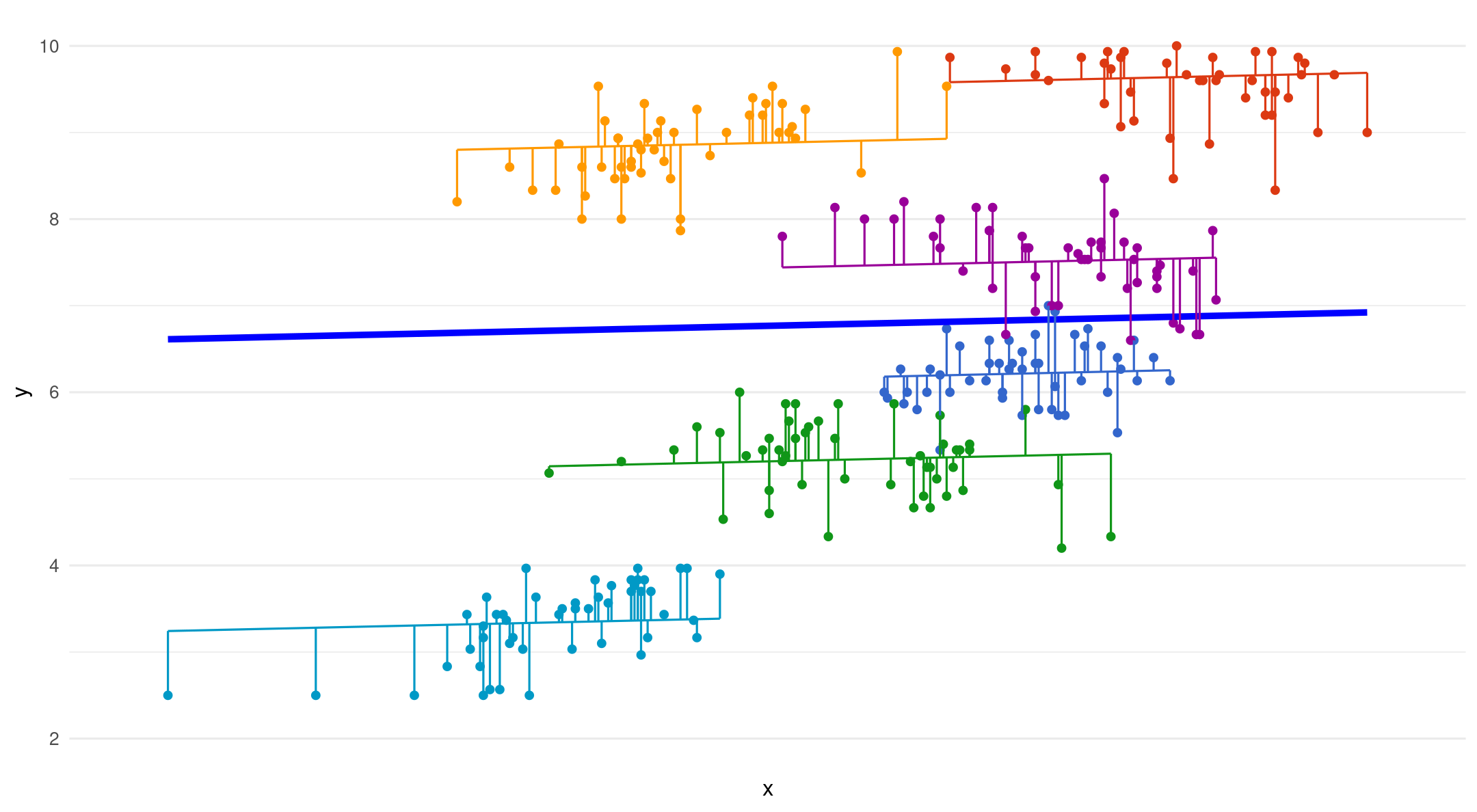
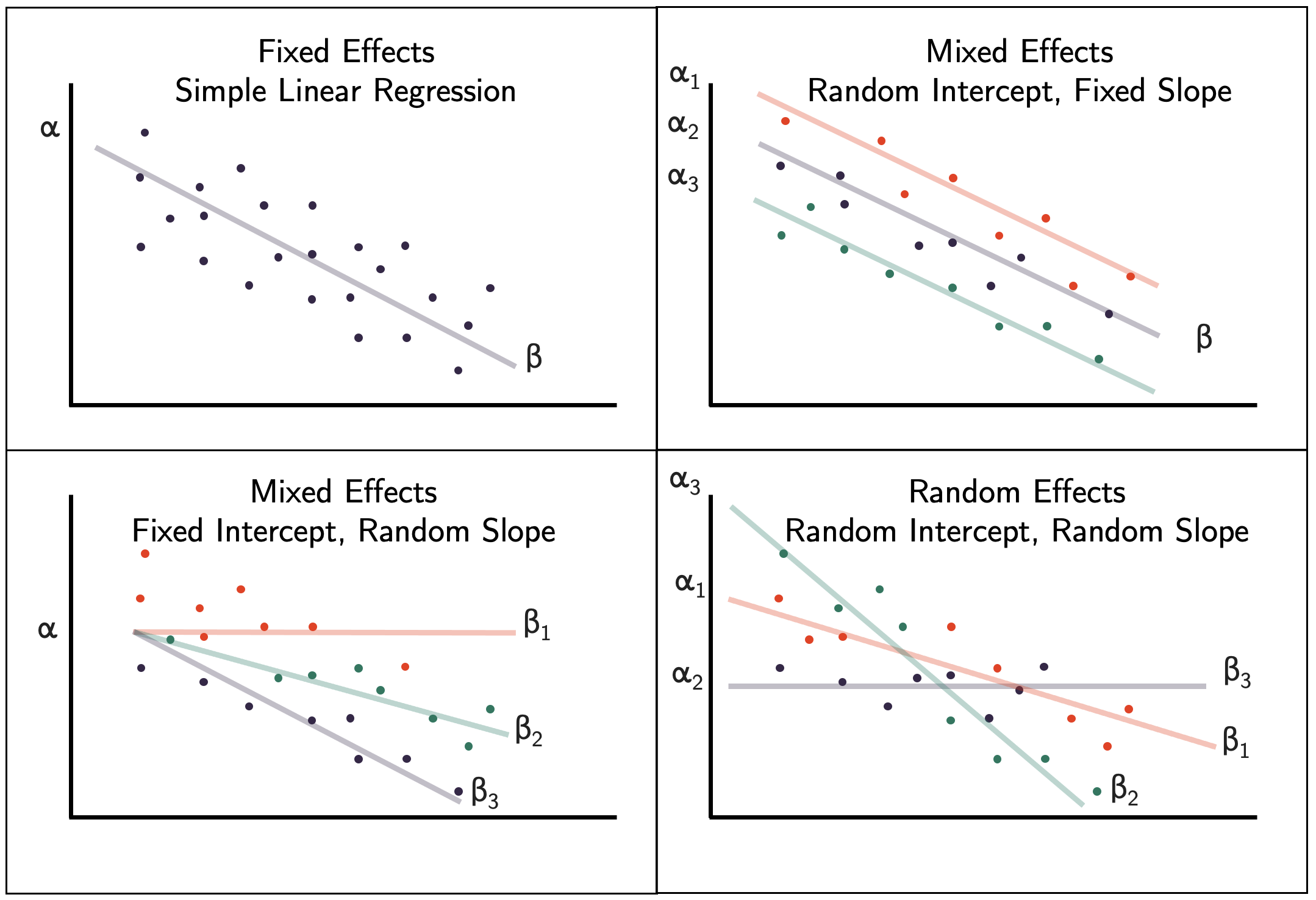
Random intercepts - fixed slope

  • Varying starting point (intercept), same slope for each group

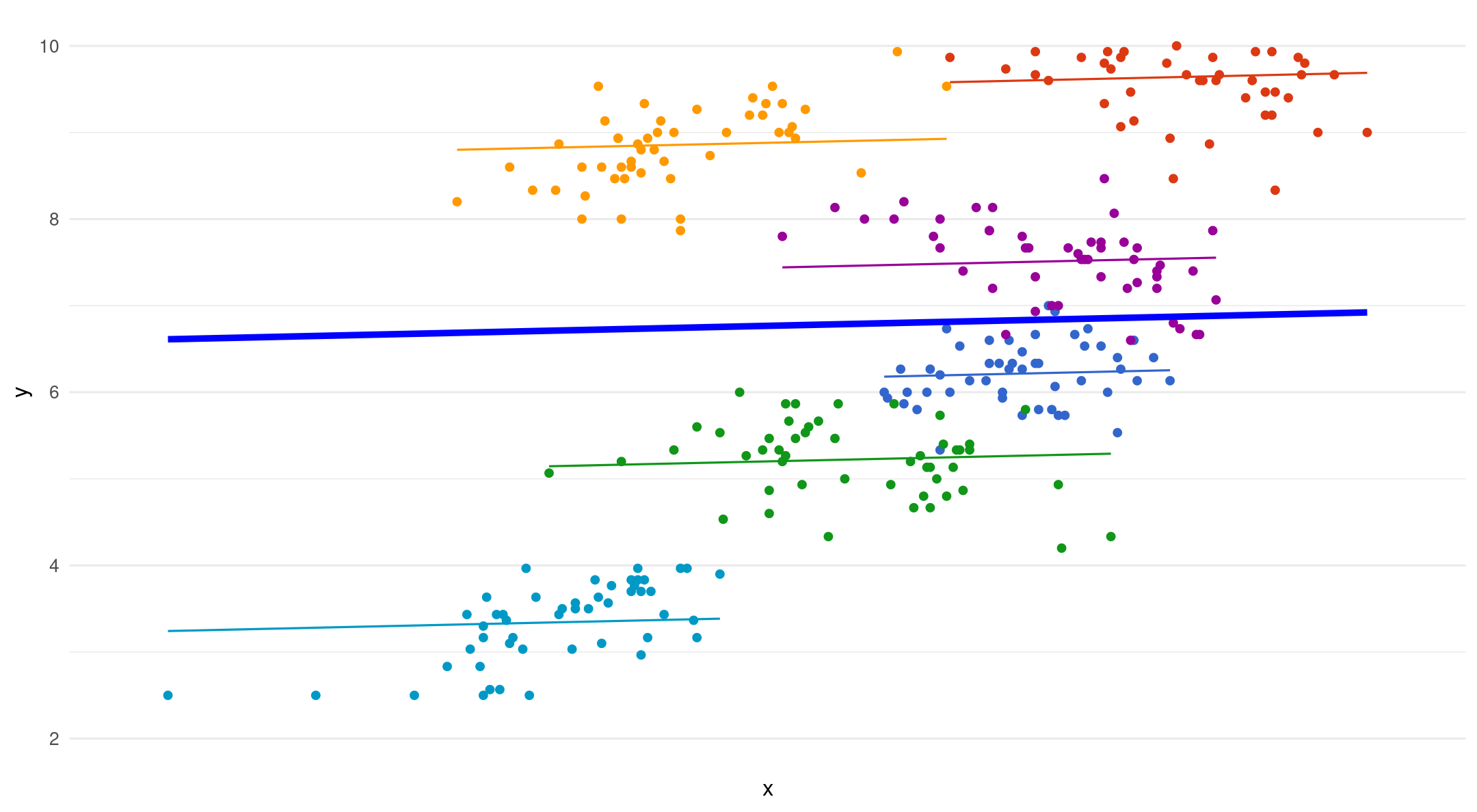
Random Intercepts - Random slopes

  • Varying starting point (intercept), varying slope for each group

\[ y_{ij} = (\color{blue}{b_{0j_{\text{(intercept)}}}} + \color{red}{U_{0j_{\text{(random intercept)}}}}) + (\color{blue}{b_{1_{\text{(slope)}}} x_{ij}} + \color{red}{U_{1j_{\text{(random slope)}}}}) + \color{red}{e_{ij_{\text{(error)}}}} \]

Important

  • Only put a random slope if it changes within cluster/group

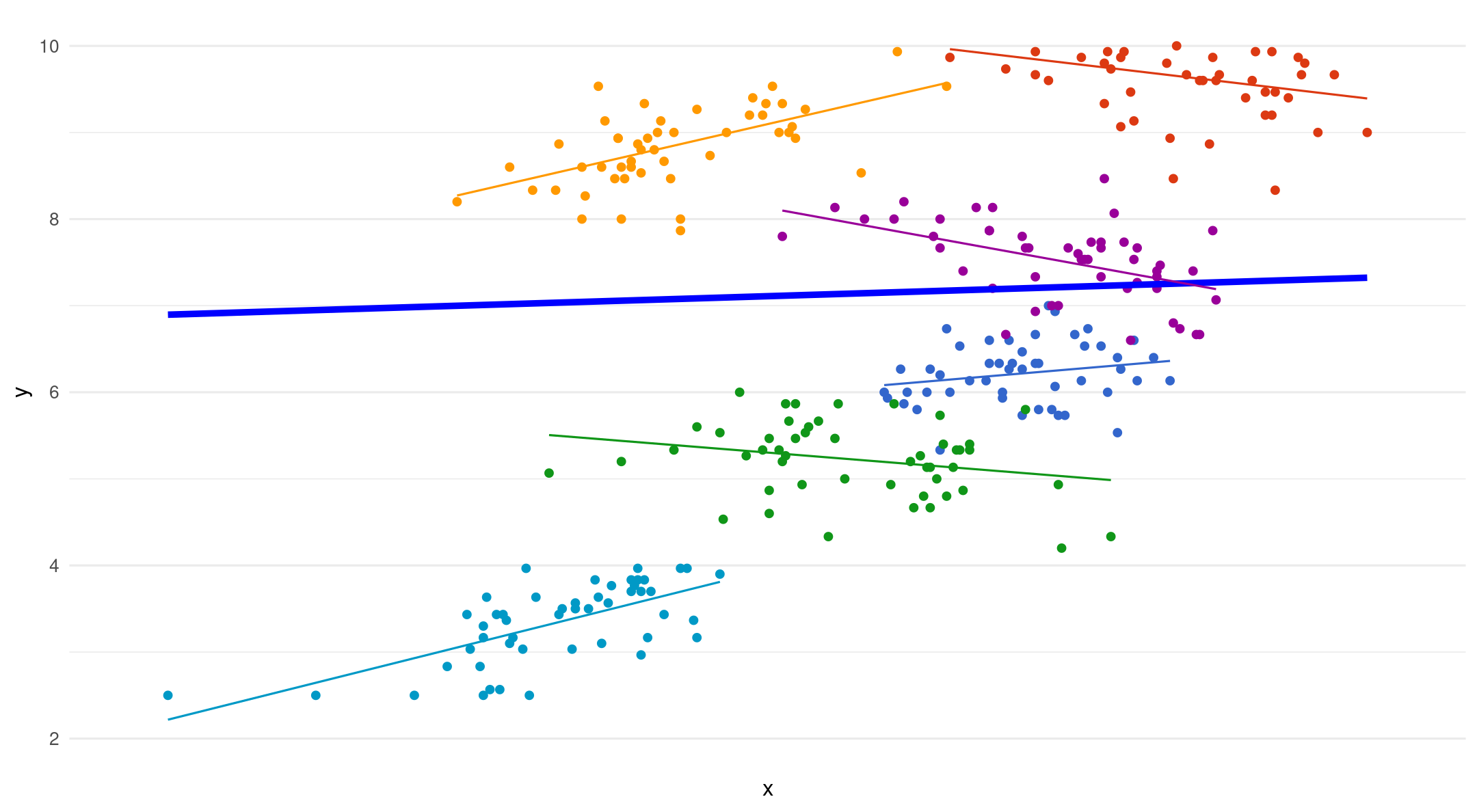
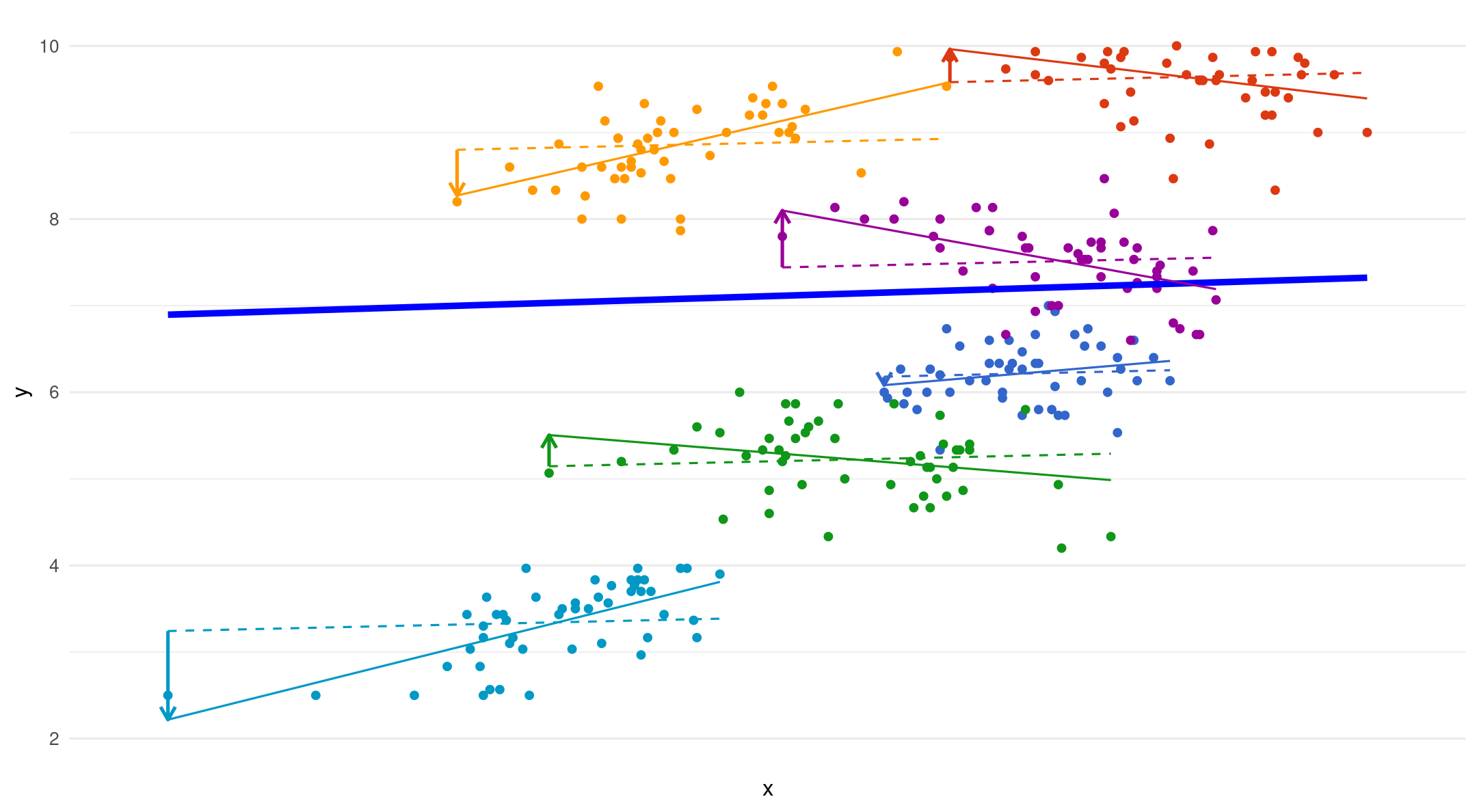
Random slopes

  • The dotted lines are fixed slopes. The arrows show the added error term for each random slope

\[ U_{1j} = b_{1j} - b_1 \]

MLM Equations

Level Equation
Level 1 \(y_{ij} = b_{0j} + b_{1j}X_{ij} + e_{ij}\)
Level 2

\(b_{0j}=γ00+U_{0j}\)

\(b_{1j} = \gamma{10} + U_{1j}\)
Combined \(y_{ij} = \gamma_{0} + \gamma_{1}X_{ij} + e_{ij} + U_{b0j} + U_{b1j}X_{ij}\)
  • You will see both equations used in the literature

All together

  • Fit models using lmer in lme4 package
lm(math~ses, data=data) # lm

lmer(math~ses + (1|schcode), data=data) # random intercept fixed slope

lmer(math~ses + (0+ ses |schcode), data=data) # random slope fixed intercept

lmer(math~ses + (1+ses|schcode), data=data) # random intercept + random slope

Syntax cheat sheet

How do your groups differ?

  • Different averages

    • Random intercept

      • Each group gets its own intercept

  • Different relationships between x and y

    • Random Slope

      • Each group gets its own slope

Implications

  • Multiple sources of variance?

    • Just add more residuals!

  • Each source of variance gets its own residual term

    • Residuals capture variance

    • Residuals are added rendering them conditionally independent

      • Otherwise, MLM is the same as GLM

How are MLMs similar to LM?

  • The fixed effects (usually) hold your hypothesis tests

    • Fixed effects output: Looks like GLM output

  • Can (essentially) be interpreted like GLM output

  • For most people, this is all that matters

How are LM and MLM different?

  • MLM has random effects output

    • Variance explained by the random effect

    • This may be interesting, in and of itself

  • Fixed effects of random terms are the average estimates across groups

Next class

PSY 504: Advaced Statistics