Missing Data in R

Princeton University

Jason Geller, PH.D.(he/him)

2024-02-11

Today

MCAR, MAR, NMAR
Screening data for missingness
Diagnosing missing data mechanisms in R
Missing data methods in R
- Listwise deletion
- Casewise deletion
- Nonconditional and conditional imputation
- Multiple imputation
- Maximum likelihood
Reporting

Packages

Install the mice package

install.packages("mice")

Load these packages:

library(tidyverse) 
library(easystats)
library(knitr)
library(broom) #tidy statistics
library(ggmice) #graph missing data
library(mice) # dealing and visualizing missing data
library(naniar) # missing data + visualization
library(finalfit)# missing data visualization

Here is the link to the .qmd document to follow along: https://github.com/jgeller112/PSY504-Advanced-Stats-S24/blob/main/slides/03-Missing_Data/03-Missing_Data.qmd.

Missing data mechanisms

Most of modern missing data theory comes from the work of statistician Donald B. Rubin
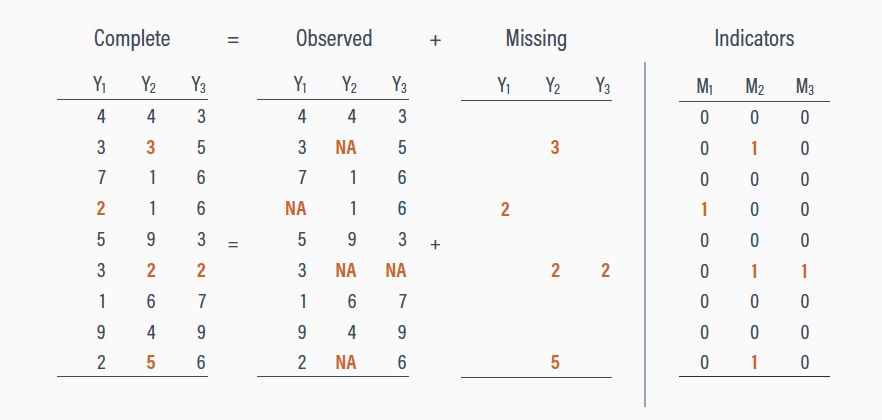
Rubin proposed we can divide an entire data set \(Y\) into two components:
- \(Y_\text{obs}\) the observed values in the data set
- \(Y_\text{mis}\) the missing values in the data set

\[Y = Y_\text{obs} + Y_\text{mis}\]

Missing data mechanisms

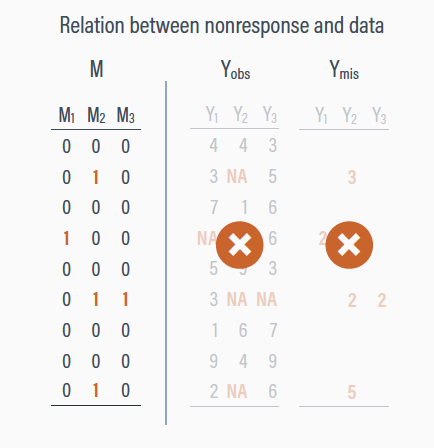
Missing data mechanisms (processes) describe different ways in which the data relate to nonresponse
Missingness may be completely random or systematically related to different parts of the data
Mechanisms function as statistical assumptions

Missing completely at random (MCAR)

The probability of missingness is unrelated to the data
MCAR is purely random missingness

Conditionally missing at random (CMAR)

Systematic missingness related to the observed scores
The probability of missing values is unrelated to the unseen (latent) data

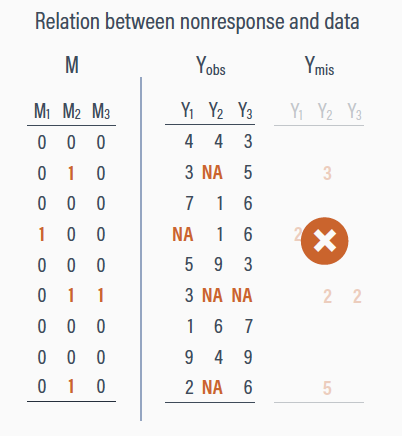
Not missing at random (NMAR)

Systematic missingness
The probability of missing values is related to the unseen (latent) data

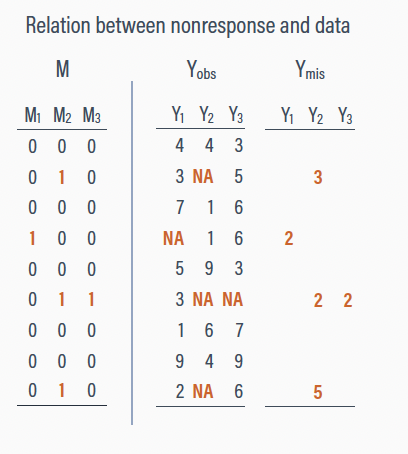
Data

Chronic pain example

Enders (2023)
- Study (N = 275) investigating psychological correlates of chronic pain
  - Depression (depress)
  - Perceived control (control)
Perceived control over pain is complete, depression scores are missing

Note

I manipulated the dataset so missingness is related to control over pain (i.e., low control is related to missingness on depression scores)

Chronic pain example

dat <- read.table("https://raw.githubusercontent.com/jgeller112/PSY504-Advanced-Stats-S24/main/slides/03-Missing_Data/APA%20Missing%20Data%20Training/Analysis%20Examples/pain.dat", na.strings = "999")

names(dat) <- c("id", "txgrp", "male", "age", "edugroup", "workhrs", "exercise", "paingrps", 
                "pain", "anxiety", "stress", "control", "depress", "interfere", "disability",
                paste0("dep", seq(1:7)), paste0("int", seq(1:6)), paste0("dis", seq(1:6)))

dat <- dat  %>%
  select("id", "age", "control",  "depress", "stress") %>%
  mutate(depress=ifelse(depress==999, NA, depress)) %>%
    mutate(r_mar_low = ifelse(control < 15.51, 1, 0)) %>% 
  mutate(depress = ifelse(r_mar_low == 1, NA, depress)) %>%
  select(-r_mar_low)

id	age	control	depress	stress
1	68	13	NA	5
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
10	31	27	NA	2
11	37	25	21	7
12	48	14	NA	4
13	33	17	20	4
14	47	13	NA	5
15	30	15	NA	1
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
24	53	14	NA	2
25	65	18	17	7
26	47	18	NA	4
27	46	20	15	4
28	34	6	NA	4
29	61	23	8	1
30	47	26	18	5
31	65	19	NA	4
32	37	14	NA	5
33	48	14	NA	6
34	41	22	24	6
35	41	14	NA	3
36	41	18	21	6
37	42	9	NA	1
38	33	24	NA	4
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
43	43	20	NA	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
51	43	13	NA	6
52	31	15	NA	1
53	45	19	13	3
54	55	24	11	7
55	50	13	NA	7
56	58	26	14	1
57	36	23	9	4
58	45	28	NA	4
59	50	24	NA	1
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
64	36	13	NA	1
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
70	46	29	NA	2
71	58	19	7	1
72	37	22	NA	4
73	46	16	12	5
74	72	24	24	5
75	32	15	NA	6
76	49	24	16	2
77	46	8	NA	6
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
81	53	27	NA	3
82	55	12	NA	4
83	23	15	NA	3
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
88	52	21	NA	4
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
103	46	13	NA	4
104	59	13	NA	1
105	28	28	8	5
106	31	14	NA	4
107	45	29	15	4
108	38	21	NA	7
109	48	25	13	5
110	32	9	NA	5
111	36	27	13	5
112	46	14	NA	5
113	65	24	15	5
114	29	21	8	3
115	34	17	NA	7
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
126	59	13	NA	6
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
143	43	17	NA	7
144	38	21	14	4
145	56	23	10	1
146	34	11	NA	4
147	67	20	NA	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
151	46	12	NA	7
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
159	48	11	NA	5
160	19	12	NA	6
161	64	25	8	2
162	65	12	NA	3
163	46	24	12	4
164	44	17	16	5
165	53	9	NA	7
166	59	16	12	3
167	60	20	21	6
168	28	13	NA	4
169	45	23	NA	2
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
175	55	27	NA	1
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
181	32	15	NA	6
182	51	17	14	4
183	78	28	NA	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
192	57	14	NA	5
193	42	22	19	7
194	37	14	NA	4
195	44	9	NA	1
196	34	19	24	3
197	31	20	NA	6
198	58	26	10	4
199	53	30	7	1
200	33	22	NA	5
201	19	7	NA	3
202	61	13	NA	4
203	42	17	NA	3
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
210	34	23	NA	4
211	49	19	NA	3
212	42	21	NA	6
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
217	34	14	NA	6
218	47	14	NA	5
219	41	19	NA	2
220	33	22	8	3
221	46	13	NA	7
222	25	14	NA	5
223	30	16	7	3
224	41	22	13	3
225	48	8	NA	7
226	42	22	26	4
227	46	20	NA	6
228	51	20	15	4
229	47	20	8	5
230	37	22	NA	1
231	30	21	28	3
232	38	29	NA	4
233	49	30	15	1
234	58	25	7	3
235	47	15	NA	5
236	55	26	NA	4
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
251	38	28	NA	1
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
262	61	19	NA	5
263	47	15	NA	3
264	45	23	NA	3
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
271	20	14	NA	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

Exploratory data analysis (EDA)

Look at your data
Need to identify missing data!
- Explore data using descriptive statistics and figures
  - What variables have missing data? How much is missing in total? By variable?

EDA

library(naniar)
vis_miss(dat)

EDA

library(skimr)
skimr::skim(dat) %>% 
  kable()

skim_type	skim_variable	n_missing	complete_rate	numeric.mean	numeric.sd	numeric.p0	numeric.p25	numeric.p50	numeric.p75	numeric.p100	numeric.hist
numeric	id	0	1.00	138.000000	79.529869	1	69.5	138	206.5	275	▇▇▇▇▇
numeric	age	0	1.00	45.643636	11.271221	19	38.0	46	53.0	78	▂▇▇▃▁
numeric	control	0	1.00	20.763636	5.252610	6	17.0	21	25.0	30	▁▃▇▇▅
numeric	depress	77	0.72	14.303030	6.058018	7	9.0	13	18.0	28	▇▆▂▂▂
numeric	stress	0	1.00	3.901818	1.802623	1	3.0	4	5.0	7	▇▅▇▅▆

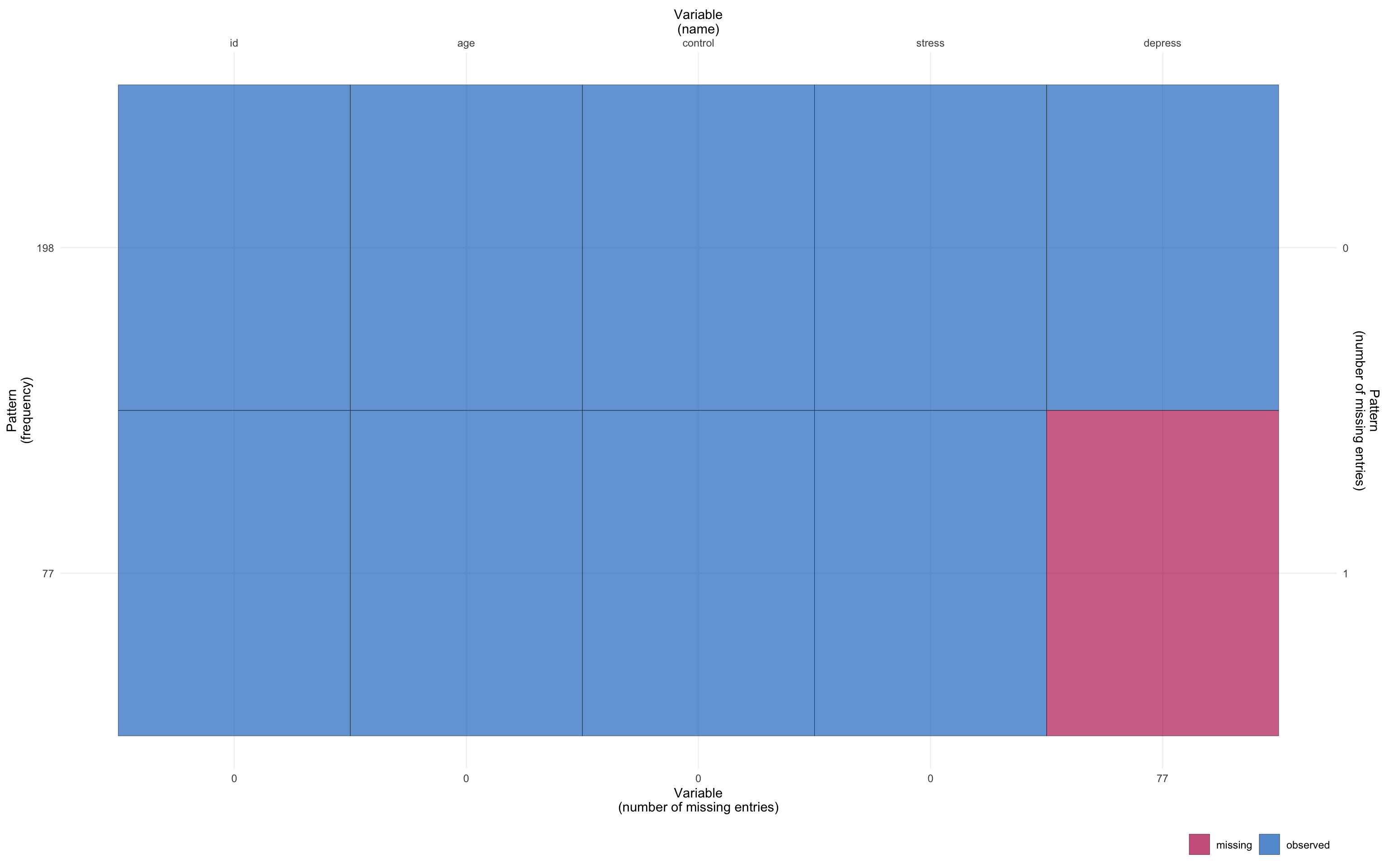
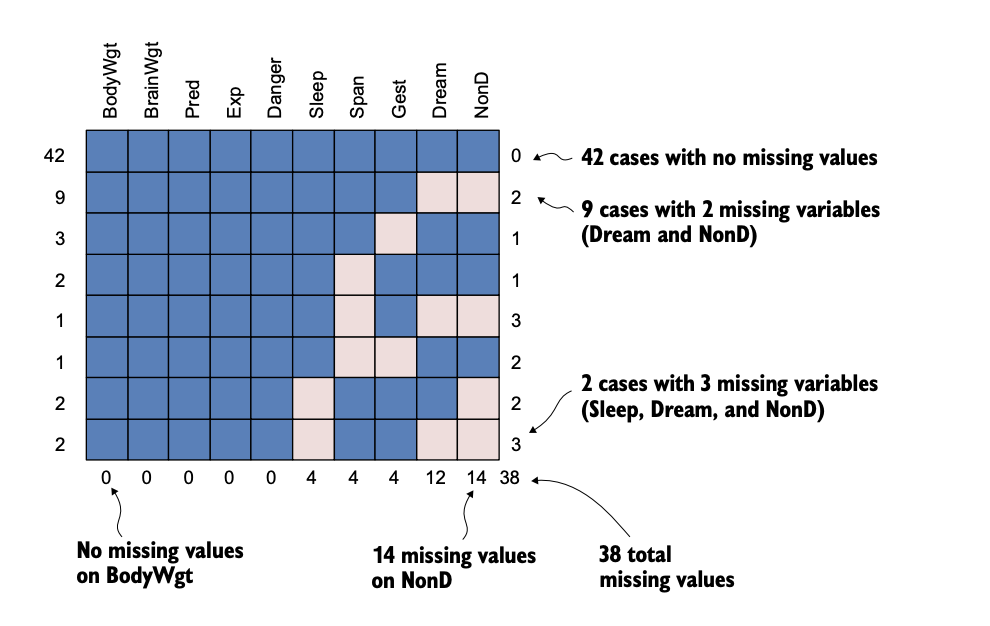
Missing patterns

A missing data pattern matrix is the structure of observed and missing values in the dataset
- Where the data is missing

#md.pattern(dat)
#ggmice
dat %>%
 # create missing data pattern plot
plot_pattern()

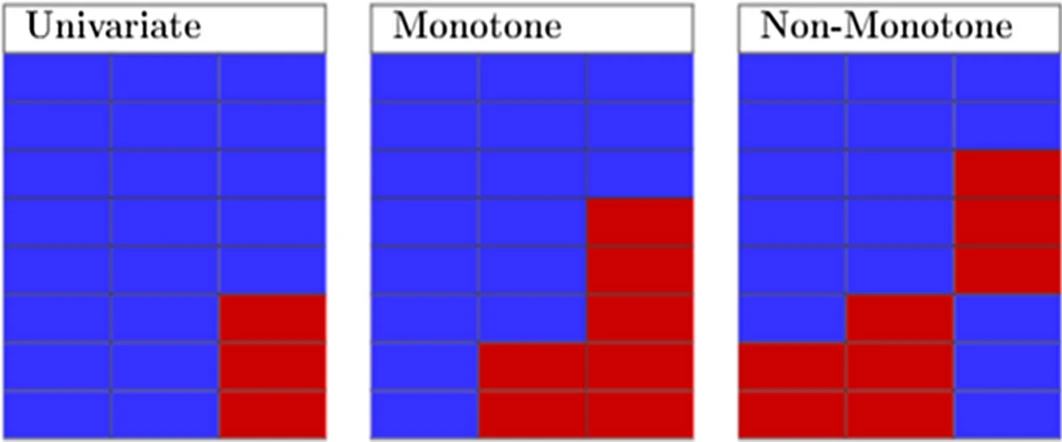
Missing patterns

Univariate: one variable with missing data
Monotone: patterns in the data can be arranged
- Associated with a longitudinal studies where members drop out and never return
Non-monotone: missingness of one variable does not affect the missingness of any other variables
- Look for islands of missingness

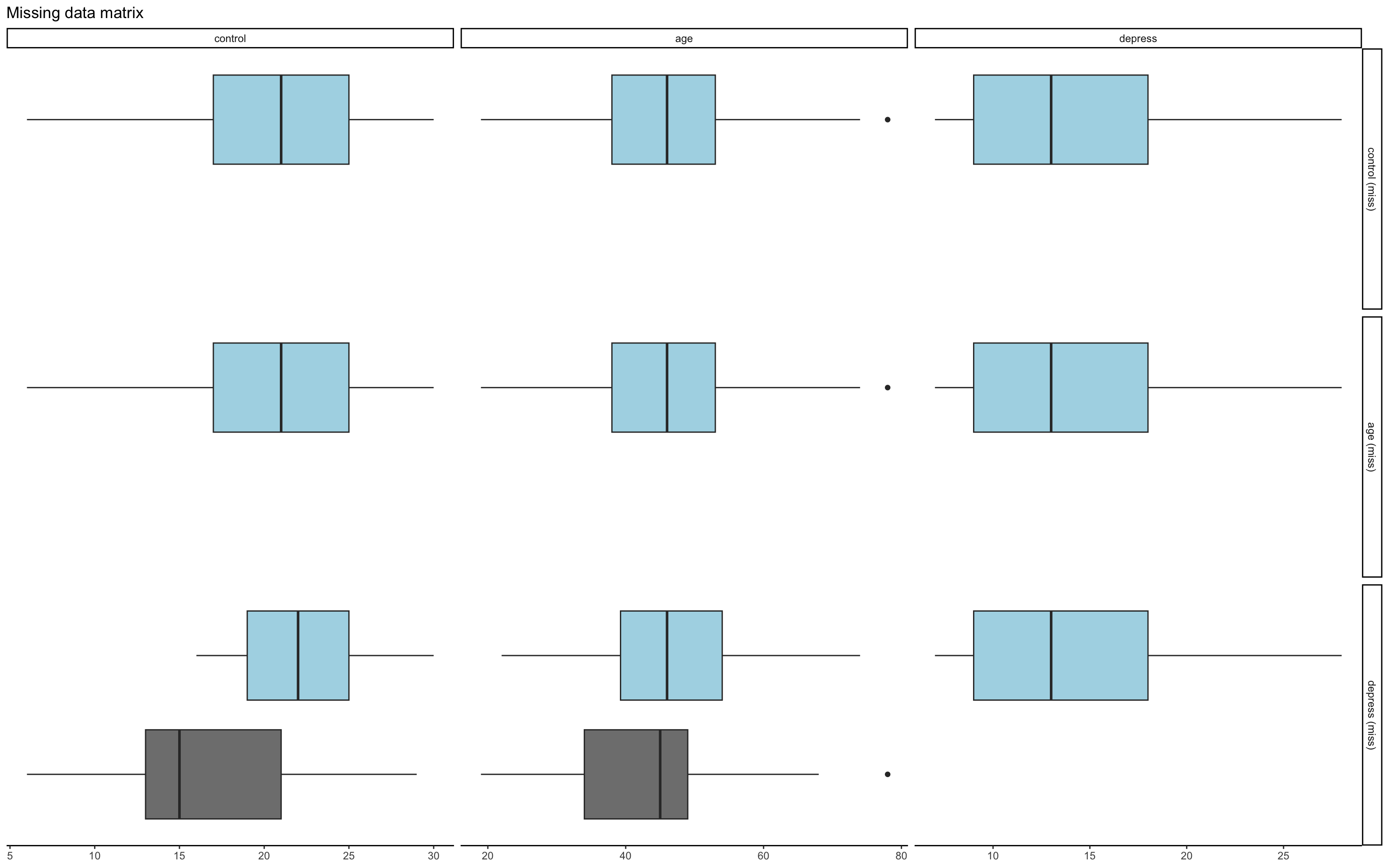
Is it MCAR or MAR?

Can make a case for MCAR
- Little’s test
  - \(\chi^2\)
    - Sig = not MCAR
    - Not sig = MCAR

library(naniar)

mcar_test(dat) %>% kable()

statistic	df	p.value	missing.patterns
66.38158	4	0	2

Not used much anymore!

Is it MCAR or MAR?

library(finalfit)

explanatory = c("control", "age")
dependent = "depress" 

misspairs <- dat %>%
  missing_pairs(explanatory, dependent)
   # mice function visualize data

Is it MCAR or MAR?

Our job is to find out if our data is MAR
- Create a dummy coded variable for missing variable where 1 = score missing and 0 = score not missing on missing variable
  - If these variables are related to other variables in dataset
    - MAR

pain_r <- dat %>%#can also use case_when #if missing 1 else 
  mutate(depress_1 = ifelse(is.na(depress), 1, 0))
pain_r %>% head() %>% kable()

id	age	control	depress	stress	depress_1
1	68	13	NA	5	1
2	38	19	28	7	0
3	31	20	8	4	0
4	31	17	28	7	0
5	58	22	12	3	0
6	63	26	13	5	0

Testing

lm or t-test

model <- lm(control~depress_1,data=pain_r)

tidy(model) %>%
  kable()

term	estimate	std.error	statistic	p.value
(Intercept)	22.348485	0.3270999	68.323107	0
depress_1	-5.660173	0.6181608	-9.156474	0

It looks like missing on depression is related to control!

Methods for dealing with MCAR

Listwise deletion

dat %>%
  kable()

id	age	control	depress	stress
1	68	13	NA	5
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
10	31	27	NA	2
11	37	25	21	7
12	48	14	NA	4
13	33	17	20	4
14	47	13	NA	5
15	30	15	NA	1
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
24	53	14	NA	2
25	65	18	17	7
26	47	18	NA	4
27	46	20	15	4
28	34	6	NA	4
29	61	23	8	1
30	47	26	18	5
31	65	19	NA	4
32	37	14	NA	5
33	48	14	NA	6
34	41	22	24	6
35	41	14	NA	3
36	41	18	21	6
37	42	9	NA	1
38	33	24	NA	4
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
43	43	20	NA	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
51	43	13	NA	6
52	31	15	NA	1
53	45	19	13	3
54	55	24	11	7
55	50	13	NA	7
56	58	26	14	1
57	36	23	9	4
58	45	28	NA	4
59	50	24	NA	1
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
64	36	13	NA	1
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
70	46	29	NA	2
71	58	19	7	1
72	37	22	NA	4
73	46	16	12	5
74	72	24	24	5
75	32	15	NA	6
76	49	24	16	2
77	46	8	NA	6
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
81	53	27	NA	3
82	55	12	NA	4
83	23	15	NA	3
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
88	52	21	NA	4
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
103	46	13	NA	4
104	59	13	NA	1
105	28	28	8	5
106	31	14	NA	4
107	45	29	15	4
108	38	21	NA	7
109	48	25	13	5
110	32	9	NA	5
111	36	27	13	5
112	46	14	NA	5
113	65	24	15	5
114	29	21	8	3
115	34	17	NA	7
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
126	59	13	NA	6
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
143	43	17	NA	7
144	38	21	14	4
145	56	23	10	1
146	34	11	NA	4
147	67	20	NA	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
151	46	12	NA	7
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
159	48	11	NA	5
160	19	12	NA	6
161	64	25	8	2
162	65	12	NA	3
163	46	24	12	4
164	44	17	16	5
165	53	9	NA	7
166	59	16	12	3
167	60	20	21	6
168	28	13	NA	4
169	45	23	NA	2
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
175	55	27	NA	1
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
181	32	15	NA	6
182	51	17	14	4
183	78	28	NA	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
192	57	14	NA	5
193	42	22	19	7
194	37	14	NA	4
195	44	9	NA	1
196	34	19	24	3
197	31	20	NA	6
198	58	26	10	4
199	53	30	7	1
200	33	22	NA	5
201	19	7	NA	3
202	61	13	NA	4
203	42	17	NA	3
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
210	34	23	NA	4
211	49	19	NA	3
212	42	21	NA	6
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
217	34	14	NA	6
218	47	14	NA	5
219	41	19	NA	2
220	33	22	8	3
221	46	13	NA	7
222	25	14	NA	5
223	30	16	7	3
224	41	22	13	3
225	48	8	NA	7
226	42	22	26	4
227	46	20	NA	6
228	51	20	15	4
229	47	20	8	5
230	37	22	NA	1
231	30	21	28	3
232	38	29	NA	4
233	49	30	15	1
234	58	25	7	3
235	47	15	NA	5
236	55	26	NA	4
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
251	38	28	NA	1
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
262	61	19	NA	5
263	47	15	NA	3
264	45	23	NA	3
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
271	20	14	NA	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

dat  %>%
  drop_na() %>%
  kable()

id	age	control	depress	stress
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
11	37	25	21	7
13	33	17	20	4
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
25	65	18	17	7
27	46	20	15	4
29	61	23	8	1
30	47	26	18	5
34	41	22	24	6
36	41	18	21	6
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
53	45	19	13	3
54	55	24	11	7
56	58	26	14	1
57	36	23	9	4
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
71	58	19	7	1
73	46	16	12	5
74	72	24	24	5
76	49	24	16	2
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
105	28	28	8	5
107	45	29	15	4
109	48	25	13	5
111	36	27	13	5
113	65	24	15	5
114	29	21	8	3
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
144	38	21	14	4
145	56	23	10	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
161	64	25	8	2
163	46	24	12	4
164	44	17	16	5
166	59	16	12	3
167	60	20	21	6
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
182	51	17	14	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
193	42	22	19	7
196	34	19	24	3
198	58	26	10	4
199	53	30	7	1
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
220	33	22	8	3
223	30	16	7	3
224	41	22	13	3
226	42	22	26	4
228	51	20	15	4
229	47	20	8	5
231	30	21	28	3
233	49	30	15	1
234	58	25	7	3
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

Listwise deletion: pros and cons

Pros:
- Produces the correct parameter estimates if missingness is MCAR
  - If not, biased
Cons:
- Can result in a lot of data loss

Casewise (pairwise) deletion

In each comparison, delete only observations if the missing data is relevant to this comparison

#create data frame
dat %>%
  kable()

id	age	control	depress	stress
1	68	13	NA	5
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
10	31	27	NA	2
11	37	25	21	7
12	48	14	NA	4
13	33	17	20	4
14	47	13	NA	5
15	30	15	NA	1
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
24	53	14	NA	2
25	65	18	17	7
26	47	18	NA	4
27	46	20	15	4
28	34	6	NA	4
29	61	23	8	1
30	47	26	18	5
31	65	19	NA	4
32	37	14	NA	5
33	48	14	NA	6
34	41	22	24	6
35	41	14	NA	3
36	41	18	21	6
37	42	9	NA	1
38	33	24	NA	4
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
43	43	20	NA	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
51	43	13	NA	6
52	31	15	NA	1
53	45	19	13	3
54	55	24	11	7
55	50	13	NA	7
56	58	26	14	1
57	36	23	9	4
58	45	28	NA	4
59	50	24	NA	1
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
64	36	13	NA	1
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
70	46	29	NA	2
71	58	19	7	1
72	37	22	NA	4
73	46	16	12	5
74	72	24	24	5
75	32	15	NA	6
76	49	24	16	2
77	46	8	NA	6
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
81	53	27	NA	3
82	55	12	NA	4
83	23	15	NA	3
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
88	52	21	NA	4
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
103	46	13	NA	4
104	59	13	NA	1
105	28	28	8	5
106	31	14	NA	4
107	45	29	15	4
108	38	21	NA	7
109	48	25	13	5
110	32	9	NA	5
111	36	27	13	5
112	46	14	NA	5
113	65	24	15	5
114	29	21	8	3
115	34	17	NA	7
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
126	59	13	NA	6
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
143	43	17	NA	7
144	38	21	14	4
145	56	23	10	1
146	34	11	NA	4
147	67	20	NA	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
151	46	12	NA	7
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
159	48	11	NA	5
160	19	12	NA	6
161	64	25	8	2
162	65	12	NA	3
163	46	24	12	4
164	44	17	16	5
165	53	9	NA	7
166	59	16	12	3
167	60	20	21	6
168	28	13	NA	4
169	45	23	NA	2
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
175	55	27	NA	1
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
181	32	15	NA	6
182	51	17	14	4
183	78	28	NA	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
192	57	14	NA	5
193	42	22	19	7
194	37	14	NA	4
195	44	9	NA	1
196	34	19	24	3
197	31	20	NA	6
198	58	26	10	4
199	53	30	7	1
200	33	22	NA	5
201	19	7	NA	3
202	61	13	NA	4
203	42	17	NA	3
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
210	34	23	NA	4
211	49	19	NA	3
212	42	21	NA	6
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
217	34	14	NA	6
218	47	14	NA	5
219	41	19	NA	2
220	33	22	8	3
221	46	13	NA	7
222	25	14	NA	5
223	30	16	7	3
224	41	22	13	3
225	48	8	NA	7
226	42	22	26	4
227	46	20	NA	6
228	51	20	15	4
229	47	20	8	5
230	37	22	NA	1
231	30	21	28	3
232	38	29	NA	4
233	49	30	15	1
234	58	25	7	3
235	47	15	NA	5
236	55	26	NA	4
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
251	38	28	NA	1
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
262	61	19	NA	5
263	47	15	NA	3
264	45	23	NA	3
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
271	20	14	NA	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

Casewise deletion: pros and cons

Pros:

Avoids data loss
Non-biased
- Only for MCAR

Cons:

But, results not completely consistent or comparable–based on different observations

Methods for MAR

Unconditional (mean) imputation - Bad

Replace missing values with the mean of the observed values
- Reduces variance
  - Increases Type 1 error rate

d <- c(5, 8, 3, NA, NA)

#calc mean remove NAs
d_mean <- mean(d, na.rm = TRUE)

d_mean_imp <- ifelse(is.na(d), d_mean, d) # add mean

d_mean_imp

[1] 5.000000 8.000000 3.000000 5.333333 5.333333

sd(d, na.rm=TRUE) # sd of org dataset

[1] 2.516611

sd(d_mean_imp) # sd of mean impute dataset

[1] 1.779513

#NANIRE Package 
#impute_mean(d) %>% head()
# Do this in Mice
#complete(mice(data, m=1, method="mean"))

Conditional imputation (regression)

Run a regression using the complete data to replace the missing value

lm(depress~control) # on complete data

imp.regress <- mice(dat, method="norm.predict", m=1, maxit=1) # norm.predict performs regression impute

All the other related variables in the data set are used to predict the values of the variable with missing data
Missing scores have the predicted values provided to replace them

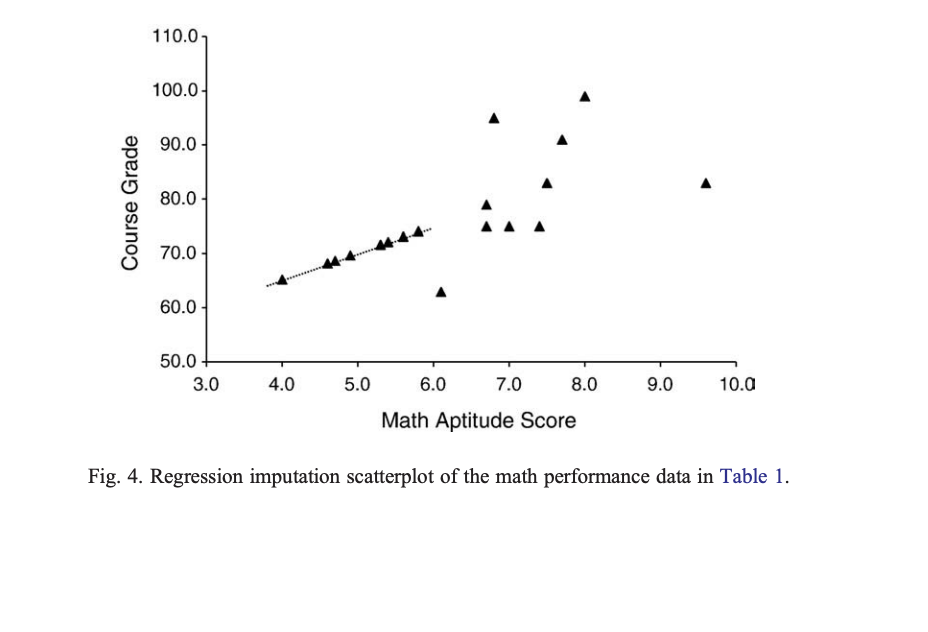
Stochastic Regression

Regression imputation with added error variance to predicted values

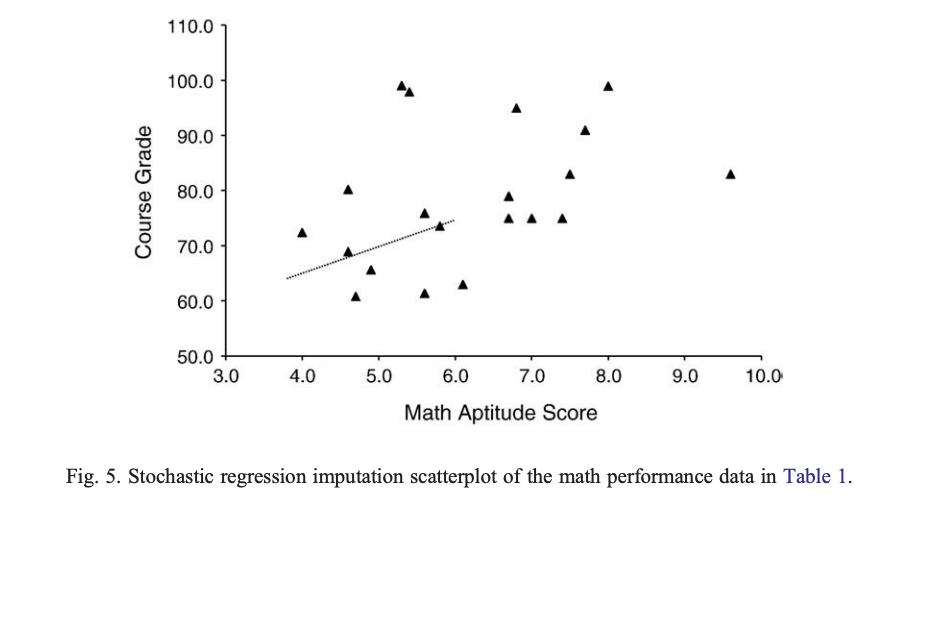
mice(data, m=1, method="norm.nob") # perfrom stoch regression

MI

Multiple Imputation

Instead of using one value as a true value (which ignores uncertainty and variance), we use multiple values
Basically doing conditional imputation several times
- Several steps

We make several multiply imputed data sets with the mice() function

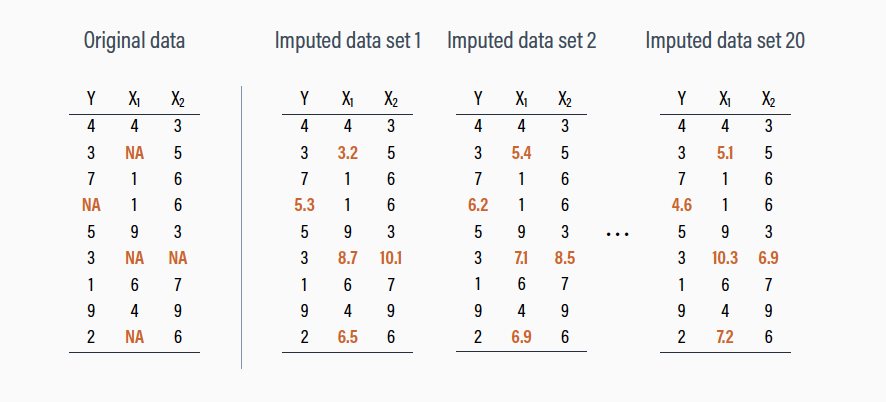
Multiple Imputation

We fit our model of choice to each version of the data with the with() function

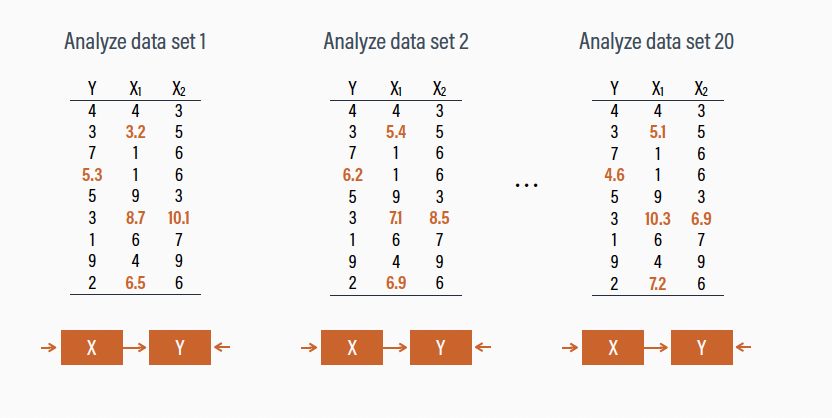
Multiple Imputation

We then pool (i.e., combine) the results with the pool() function

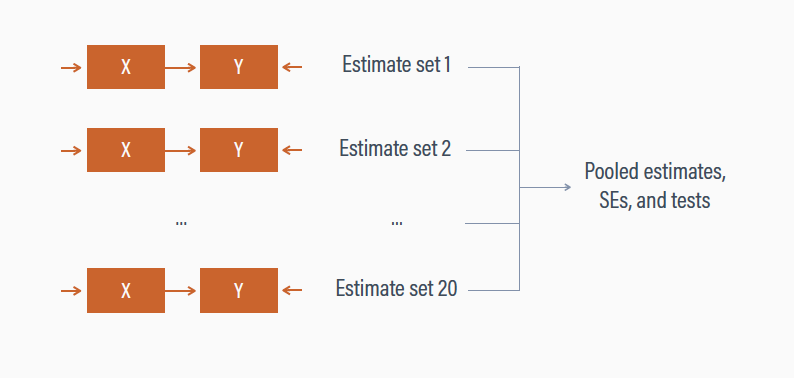
Multiple Imputation

1. Impute with `Mice`

m=5
# impute several data sets
imp <- mice(dat, m = m, seed = 24415, method="pmm", print = FALSE)

What is imp?

str(imp, max.level = 1)

List of 22
 $ data           :'data.frame':    275 obs. of  5 variables:
 $ imp            :List of 5
 $ m              : num 5
 $ where          : logi [1:275, 1:5] FALSE FALSE FALSE FALSE FALSE FALSE ...
  ..- attr(*, "dimnames")=List of 2
 $ blocks         :List of 5
  ..- attr(*, "calltype")= Named chr [1:5] "type" "type" "type" "type" ...
  .. ..- attr(*, "names")= chr [1:5] "id" "age" "control" "depress" ...
 $ call           : language mice(data = dat, m = m, method = "pmm", printFlag = FALSE, seed = 24415)
 $ nmis           : Named int [1:5] 0 0 0 77 0
  ..- attr(*, "names")= chr [1:5] "id" "age" "control" "depress" ...
 $ method         : Named chr [1:5] "" "" "" "pmm" ...
  ..- attr(*, "names")= chr [1:5] "id" "age" "control" "depress" ...
 $ predictorMatrix: num [1:5, 1:5] 0 1 1 1 1 1 0 1 1 1 ...
  ..- attr(*, "dimnames")=List of 2
 $ visitSequence  : chr [1:5] "id" "age" "control" "depress" ...
 $ formulas       :List of 5
 $ post           : Named chr [1:5] "" "" "" "" ...
  ..- attr(*, "names")= chr [1:5] "id" "age" "control" "depress" ...
 $ blots          :List of 5
 $ ignore         : logi [1:275] FALSE FALSE FALSE FALSE FALSE FALSE ...
 $ seed           : num 24415
 $ iteration      : num 5
 $ lastSeedValue  : int [1:626] 10403 359 1009391010 -1973990381 908174720 -738124646 251387381 -1899514340 395796544 1088258267 ...
 $ chainMean      : num [1:5, 1:5, 1:5] NaN NaN NaN 16.8 NaN ...
  ..- attr(*, "dimnames")=List of 3
 $ chainVar       : num [1:5, 1:5, 1:5] NA NA NA 47.1 NA ...
  ..- attr(*, "dimnames")=List of 3
 $ loggedEvents   : NULL
 $ version        :Classes 'package_version', 'numeric_version'  hidden list of 1
 $ date           : Date[1:1], format: "2024-02-11"
 - attr(*, "class")= chr "mids"

1. Impute with `Mice`

What is imp within imp?

str(imp$imp, max.level = 1)

List of 5
 $ id     :'data.frame':    0 obs. of  5 variables:
 $ age    :'data.frame':    0 obs. of  5 variables:
 $ control:'data.frame':    0 obs. of  5 variables:
 $ depress:'data.frame':    77 obs. of  5 variables:
 $ stress :'data.frame':    0 obs. of  5 variables:

#get the imputed values for that var
head(imp$imp$depress)

    1  2  3  4  5
1  28 26 18 21 13
10 12  7  8 14  8
12 19 23 10 11 27
14 24 27 20 21 27
15 19 14 15 14 12
24 26 13  8 13 12

#get the imputed datasets out
#complete(imp, "all")

PMM

Predictive mean matching
- For each missing value, a regression model is fitted using the observed (complete) data, where the variable with missing data is the outcome and other variables are predictors
- For a record with a missing value, the fitted model predicts a mean based on the available data

PMM identifies a set of “donors” from the observed data. These donors are the cases whose predicted means are closest to the predicted mean of the case with the missing value

2. Model with `Mice`

We’ll fit a simple statistical model

#fit the model to each set of imputaed data

fit <- with(data = imp, expr = lm(depress ~ control))

summary(fit) %>%
  kable()

term	estimate	std.error	statistic	nobs
(Intercept)	26.5853480	1.3951117	19.056071	275
control	-0.5579633	0.0651453	-8.564900	275
(Intercept)	26.3445428	1.4404262	18.289409	275
control	-0.5397109	0.0672613	-8.024091	275
(Intercept)	24.9087161	1.4261998	17.465096	275
control	-0.4880730	0.0665970	-7.328753	275
(Intercept)	24.3346289	1.3947519	17.447282	275
control	-0.4644524	0.0651285	-7.131319	275
(Intercept)	24.9290442	1.3967357	17.848076	275
control	-0.4862499	0.0652212	-7.455400	275

3. `Mice` Pool Results

#combine the results
result <- pool(fit)

model_parameters(result) %>%
  kable()

Parameter	Coefficient	SE	CI	CI_low	CI_high	t	df_error	p
(Intercept)	25.4204560	1.7771524	0.95	21.7601261	29.080786	14.30404	24.97094	0e+00
control	-0.5072899	0.0788639	0.95	-0.6673029	-0.347277	-6.43247	35.55542	2e-07

3. `Mice` Pool Results

emmeans does not play nicely with mice objects
marginaleffects
- Can be used to perform hypothesis tests on coefficients

library(marginaleffects)

mfx_mice <- avg_slopes(fit) # avg_comparions for categorical vars

mfx_mice %>% kable()

term	estimate	std.error	s.value	df	statistic	p.value	conf.low	conf.high
control	-0.5072899	0.0788641	23.58331	43.78869	-6.432457	1e-07	-0.6662517	-0.3483281

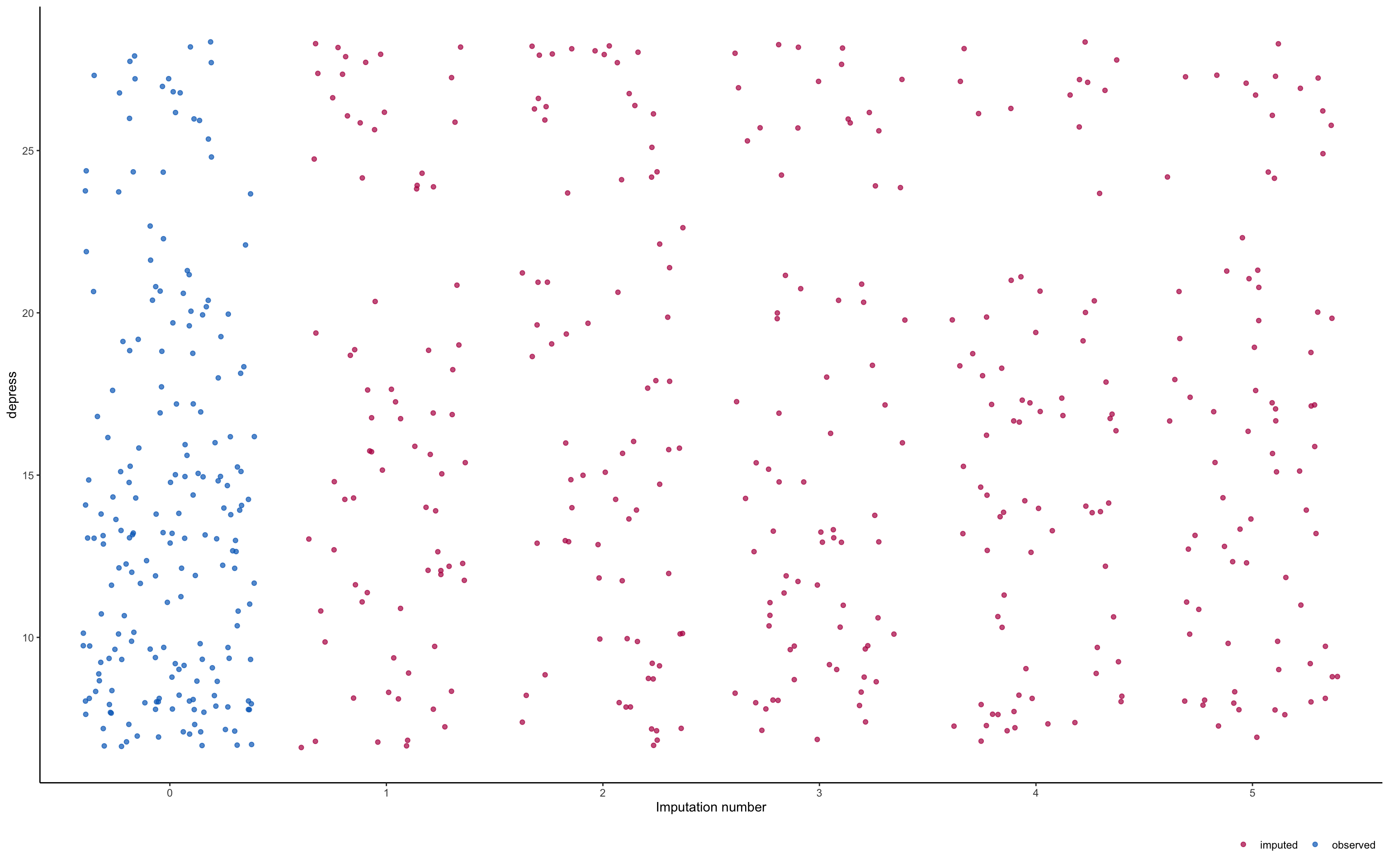
Plot Imputations

Make sure they look similar to real data

# create stripplot 
ggmice(imp, ggplot2::aes(x = .imp, y = depress)) +
  ggplot2::geom_jitter() + 
    labs(x = "Imputation number")

Maximum likelihood (ML)

ML

Determines the most probable settings (parameter estimates) for a statistical model by making the model’s predicted outcomes as close as possible to the observed data
Each observation’s contribution to estimation is restricted to the subset of parameters for which there is data
Estimation uses incomplete data, no imputation performed

ML

Implicit imputation

Each participant contributes their observed data
Data are not filled in, but the multivariate normal distribution acts like an imputation machine
The location of the observed data implies the probable position of the unseen data, and estimates are adjusted accordingly

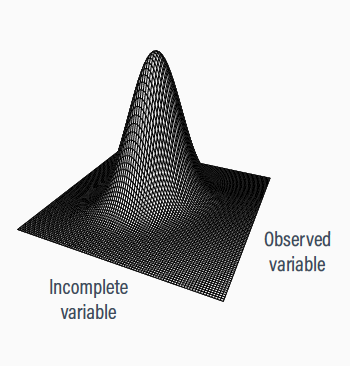
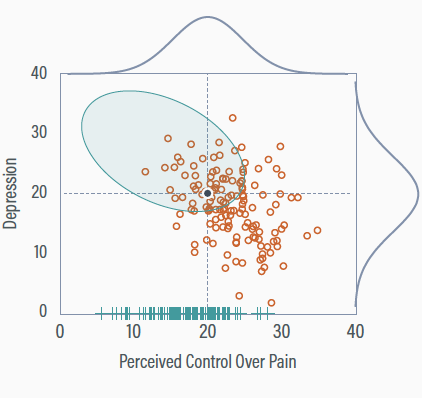
Chronic pain illustration

Participants with low perceived control are more likely to have missing depression scores (conditionally MAR)
The true means are both 20

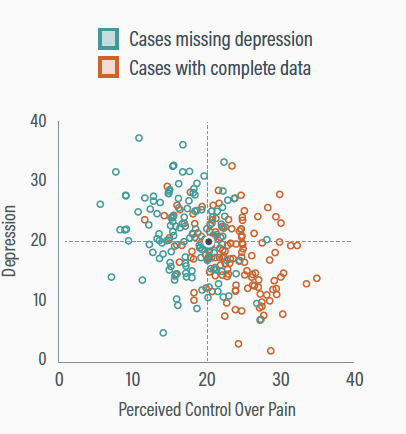
Deleting incomplete information

Deleting cases with missing depression scores gives a non-representative sample
The perceived control mean is too high (Mpc = 23.1), and the depression mean is too low (Mdep = 17.2)

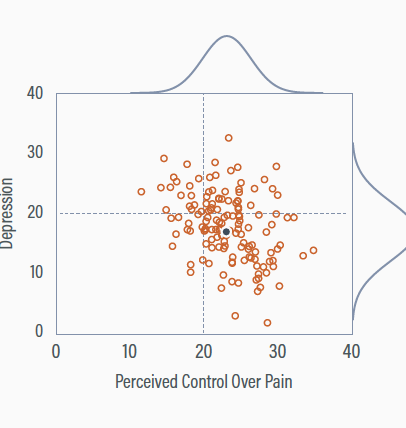
Partial data

Incorporating the partial data gives a complete set of perceived control scores
The partial data records primarily have low perceived control scores

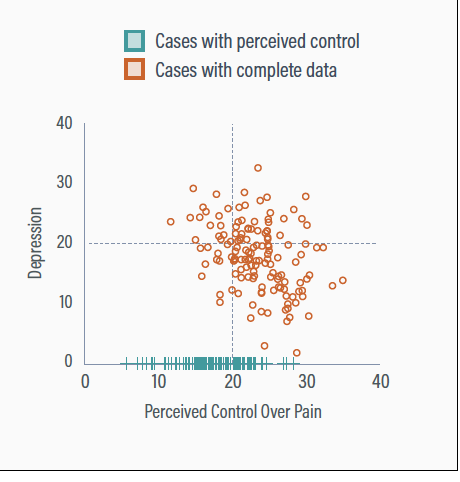
Adjusting perceived control

Adding low perceived control scores increases the variable’s variability
The perceived control mean receives a downward adjustment to accommodate the influx of low scores

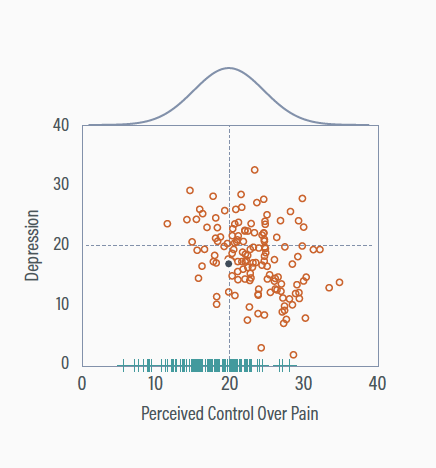
Implicit Imputation

Maximum likelihood assumes multivariate normality
In a normal distribution with a negative correlation, low perceived control scores should pair with high depression

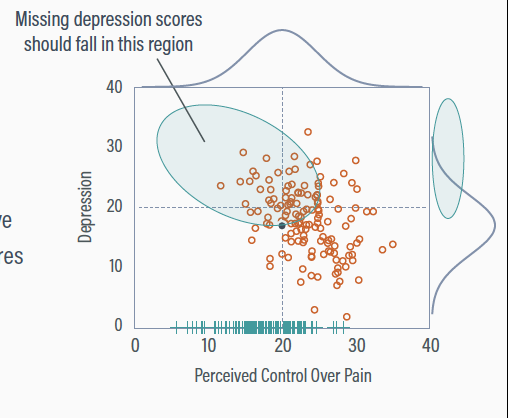
Adjusting Depression Distribution

Maximum likelihood intuits the presence of the elevated but unseen depression scores
The mean and variance of depression increase to accommodate observed perceived control scores at the low end

ML: Cons

Generally limited to normal data, options for mixed metrics are less common
Normal-theory methods are biased with interactions and non-linear terms
MLM software usually discards observations with missing predictors

Distinguish between NMAR and MAR

Pray you don’t have to 😂
It’s complicated
- Not many good techniques
NMAR into MAR
- Try and track down the missing data
- Auxiliary variables
- Collect more data for explaining missingness

Distinguish between NMAR and MAR

Reporting Missing Data

Template from Stepf van Buuren

Tip

The percentage of missing values across the nine variables varied between 0 and 34%. In total 1601 out of 3801 records (42%) were incomplete. Many girls had no score because the nurse felt that the measurement was “unnecessary,” or because the girl did not give permission. Older girls had many more missing data. We used multiple imputation to create and analyze 40 multiply imputed datasets. Methodologists currently regard multiple imputation as a state-of-the-art technique because it improves accuracy and statistical power relative to other missing data techniques. Incomplete variables were imputed under fully conditional specification, using the default settings of the mice 3.0 package (Van Buuren and Groothuis-Oudshoorn 2011). The parameters of substantive interest were estimated in each imputed dataset separately, and combined using Rubin’s rules. For comparison, we also performed the analysis on the subset of complete cases.

Report

Amount of missing data
Reasons for missingness
Consequences
Method
Imputation model
Pooling
Software
Complete-case analysis

Is it MCAR, MAR, NMAR?

The post-experiment manipulation-check questionnaires for five participants were accidentally thrown away.

MCAR

Is it MCAR, MAR, NMAR?

In a 2-day memory experiment, people who know they would do poorly on the memory test are discouraged and don’t want to return for the second session

NMAR

Is it MCAR, MAR, NMAR?

A health psychologist is surveying high school students on marijuana use. Students who scored highly on anxiety left these questions blank.

Wrap up

When you have missing data, think about WHY they are missing
Missing data handled improperly can bias your expectations
MI and ML are good ways to handle missing data!
- Bayesian methods are good too :)
- Inverse probability weighting seem to work well (Gomila and Clark 2022)

Gomila, Robin, and Chelsey S. Clark. 2022. “Missing Data in Experiments: Challenges and Solutions.” Psychological Methods 27 (2): 143–55. https://doi.org/10.1037/met0000361.

id	age	control	depress	stress
1	68	13	NA	5
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
10	31	27	NA	2
11	37	25	21	7
12	48	14	NA	4
13	33	17	20	4
14	47	13	NA	5
15	30	15	NA	1
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
24	53	14	NA	2
25	65	18	17	7
26	47	18	NA	4
27	46	20	15	4
28	34	6	NA	4
29	61	23	8	1
30	47	26	18	5
31	65	19	NA	4
32	37	14	NA	5
33	48	14	NA	6
34	41	22	24	6
35	41	14	NA	3
36	41	18	21	6
37	42	9	NA	1
38	33	24	NA	4
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
43	43	20	NA	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
51	43	13	NA	6
52	31	15	NA	1
53	45	19	13	3
54	55	24	11	7
55	50	13	NA	7
56	58	26	14	1
57	36	23	9	4
58	45	28	NA	4
59	50	24	NA	1
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
64	36	13	NA	1
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
70	46	29	NA	2
71	58	19	7	1
72	37	22	NA	4
73	46	16	12	5
74	72	24	24	5
75	32	15	NA	6
76	49	24	16	2
77	46	8	NA	6
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
81	53	27	NA	3
82	55	12	NA	4
83	23	15	NA	3
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
88	52	21	NA	4
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
103	46	13	NA	4
104	59	13	NA	1
105	28	28	8	5
106	31	14	NA	4
107	45	29	15	4
108	38	21	NA	7
109	48	25	13	5
110	32	9	NA	5
111	36	27	13	5
112	46	14	NA	5
113	65	24	15	5
114	29	21	8	3
115	34	17	NA	7
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
126	59	13	NA	6
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
143	43	17	NA	7
144	38	21	14	4
145	56	23	10	1
146	34	11	NA	4
147	67	20	NA	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
151	46	12	NA	7
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
159	48	11	NA	5
160	19	12	NA	6
161	64	25	8	2
162	65	12	NA	3
163	46	24	12	4
164	44	17	16	5
165	53	9	NA	7
166	59	16	12	3
167	60	20	21	6
168	28	13	NA	4
169	45	23	NA	2
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
175	55	27	NA	1
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
181	32	15	NA	6
182	51	17	14	4
183	78	28	NA	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
192	57	14	NA	5
193	42	22	19	7
194	37	14	NA	4
195	44	9	NA	1
196	34	19	24	3
197	31	20	NA	6
198	58	26	10	4
199	53	30	7	1
200	33	22	NA	5
201	19	7	NA	3
202	61	13	NA	4
203	42	17	NA	3
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
210	34	23	NA	4
211	49	19	NA	3
212	42	21	NA	6
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
217	34	14	NA	6
218	47	14	NA	5
219	41	19	NA	2
220	33	22	8	3
221	46	13	NA	7
222	25	14	NA	5
223	30	16	7	3
224	41	22	13	3
225	48	8	NA	7
226	42	22	26	4
227	46	20	NA	6
228	51	20	15	4
229	47	20	8	5
230	37	22	NA	1
231	30	21	28	3
232	38	29	NA	4
233	49	30	15	1
234	58	25	7	3
235	47	15	NA	5
236	55	26	NA	4
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
251	38	28	NA	1
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
262	61	19	NA	5
263	47	15	NA	3
264	45	23	NA	3
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
271	20	14	NA	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

id	age	control	depress	stress
1	68	13	NA	5
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
10	31	27	NA	2
11	37	25	21	7
12	48	14	NA	4
13	33	17	20	4
14	47	13	NA	5
15	30	15	NA	1
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
24	53	14	NA	2
25	65	18	17	7
26	47	18	NA	4
27	46	20	15	4
28	34	6	NA	4
29	61	23	8	1
30	47	26	18	5
31	65	19	NA	4
32	37	14	NA	5
33	48	14	NA	6
34	41	22	24	6
35	41	14	NA	3
36	41	18	21	6
37	42	9	NA	1
38	33	24	NA	4
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
43	43	20	NA	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
51	43	13	NA	6
52	31	15	NA	1
53	45	19	13	3
54	55	24	11	7
55	50	13	NA	7
56	58	26	14	1
57	36	23	9	4
58	45	28	NA	4
59	50	24	NA	1
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
64	36	13	NA	1
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
70	46	29	NA	2
71	58	19	7	1
72	37	22	NA	4
73	46	16	12	5
74	72	24	24	5
75	32	15	NA	6
76	49	24	16	2
77	46	8	NA	6
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
81	53	27	NA	3
82	55	12	NA	4
83	23	15	NA	3
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
88	52	21	NA	4
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
103	46	13	NA	4
104	59	13	NA	1
105	28	28	8	5
106	31	14	NA	4
107	45	29	15	4
108	38	21	NA	7
109	48	25	13	5
110	32	9	NA	5
111	36	27	13	5
112	46	14	NA	5
113	65	24	15	5
114	29	21	8	3
115	34	17	NA	7
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
126	59	13	NA	6
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
143	43	17	NA	7
144	38	21	14	4
145	56	23	10	1
146	34	11	NA	4
147	67	20	NA	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
151	46	12	NA	7
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
159	48	11	NA	5
160	19	12	NA	6
161	64	25	8	2
162	65	12	NA	3
163	46	24	12	4
164	44	17	16	5
165	53	9	NA	7
166	59	16	12	3
167	60	20	21	6
168	28	13	NA	4
169	45	23	NA	2
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
175	55	27	NA	1
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
181	32	15	NA	6
182	51	17	14	4
183	78	28	NA	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
192	57	14	NA	5
193	42	22	19	7
194	37	14	NA	4
195	44	9	NA	1
196	34	19	24	3
197	31	20	NA	6
198	58	26	10	4
199	53	30	7	1
200	33	22	NA	5
201	19	7	NA	3
202	61	13	NA	4
203	42	17	NA	3
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
210	34	23	NA	4
211	49	19	NA	3
212	42	21	NA	6
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
217	34	14	NA	6
218	47	14	NA	5
219	41	19	NA	2
220	33	22	8	3
221	46	13	NA	7
222	25	14	NA	5
223	30	16	7	3
224	41	22	13	3
225	48	8	NA	7
226	42	22	26	4
227	46	20	NA	6
228	51	20	15	4
229	47	20	8	5
230	37	22	NA	1
231	30	21	28	3
232	38	29	NA	4
233	49	30	15	1
234	58	25	7	3
235	47	15	NA	5
236	55	26	NA	4
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
251	38	28	NA	1
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
262	61	19	NA	5
263	47	15	NA	3
264	45	23	NA	3
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
271	20	14	NA	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

id	age	control	depress	stress
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
11	37	25	21	7
13	33	17	20	4
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
25	65	18	17	7
27	46	20	15	4
29	61	23	8	1
30	47	26	18	5
34	41	22	24	6
36	41	18	21	6
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
53	45	19	13	3
54	55	24	11	7
56	58	26	14	1
57	36	23	9	4
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
71	58	19	7	1
73	46	16	12	5
74	72	24	24	5
76	49	24	16	2
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
105	28	28	8	5
107	45	29	15	4
109	48	25	13	5
111	36	27	13	5
113	65	24	15	5
114	29	21	8	3
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
144	38	21	14	4
145	56	23	10	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
161	64	25	8	2
163	46	24	12	4
164	44	17	16	5
166	59	16	12	3
167	60	20	21	6
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
182	51	17	14	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
193	42	22	19	7
196	34	19	24	3
198	58	26	10	4
199	53	30	7	1
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
220	33	22	8	3
223	30	16	7	3
224	41	22	13	3
226	42	22	26	4
228	51	20	15	4
229	47	20	8	5
231	30	21	28	3
233	49	30	15	1
234	58	25	7	3
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

id	age	control	depress	stress
1	68	13	NA	5
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
10	31	27	NA	2
11	37	25	21	7
12	48	14	NA	4
13	33	17	20	4
14	47	13	NA	5
15	30	15	NA	1
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
24	53	14	NA	2
25	65	18	17	7
26	47	18	NA	4
27	46	20	15	4
28	34	6	NA	4
29	61	23	8	1
30	47	26	18	5
31	65	19	NA	4
32	37	14	NA	5
33	48	14	NA	6
34	41	22	24	6
35	41	14	NA	3
36	41	18	21	6
37	42	9	NA	1
38	33	24	NA	4
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
43	43	20	NA	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
51	43	13	NA	6
52	31	15	NA	1
53	45	19	13	3
54	55	24	11	7
55	50	13	NA	7
56	58	26	14	1
57	36	23	9	4
58	45	28	NA	4
59	50	24	NA	1
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
64	36	13	NA	1
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
70	46	29	NA	2
71	58	19	7	1
72	37	22	NA	4
73	46	16	12	5
74	72	24	24	5
75	32	15	NA	6
76	49	24	16	2
77	46	8	NA	6
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
81	53	27	NA	3
82	55	12	NA	4
83	23	15	NA	3
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
88	52	21	NA	4
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
103	46	13	NA	4
104	59	13	NA	1
105	28	28	8	5
106	31	14	NA	4
107	45	29	15	4
108	38	21	NA	7
109	48	25	13	5
110	32	9	NA	5
111	36	27	13	5
112	46	14	NA	5
113	65	24	15	5
114	29	21	8	3
115	34	17	NA	7
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
126	59	13	NA	6
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
143	43	17	NA	7
144	38	21	14	4
145	56	23	10	1
146	34	11	NA	4
147	67	20	NA	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
151	46	12	NA	7
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
159	48	11	NA	5
160	19	12	NA	6
161	64	25	8	2
162	65	12	NA	3
163	46	24	12	4
164	44	17	16	5
165	53	9	NA	7
166	59	16	12	3
167	60	20	21	6
168	28	13	NA	4
169	45	23	NA	2
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
175	55	27	NA	1
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
181	32	15	NA	6
182	51	17	14	4
183	78	28	NA	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
192	57	14	NA	5
193	42	22	19	7
194	37	14	NA	4
195	44	9	NA	1
196	34	19	24	3
197	31	20	NA	6
198	58	26	10	4
199	53	30	7	1
200	33	22	NA	5
201	19	7	NA	3
202	61	13	NA	4
203	42	17	NA	3
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
210	34	23	NA	4
211	49	19	NA	3
212	42	21	NA	6
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
217	34	14	NA	6
218	47	14	NA	5
219	41	19	NA	2
220	33	22	8	3
221	46	13	NA	7
222	25	14	NA	5
223	30	16	7	3
224	41	22	13	3
225	48	8	NA	7
226	42	22	26	4
227	46	20	NA	6
228	51	20	15	4
229	47	20	8	5
230	37	22	NA	1
231	30	21	28	3
232	38	29	NA	4
233	49	30	15	1
234	58	25	7	3
235	47	15	NA	5
236	55	26	NA	4
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
251	38	28	NA	1
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
262	61	19	NA	5
263	47	15	NA	3
264	45	23	NA	3
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
271	20	14	NA	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

id	age	control	depress	stress
1	68	13	NA	5
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
10	31	27	NA	2
11	37	25	21	7
12	48	14	NA	4
13	33	17	20	4
14	47	13	NA	5
15	30	15	NA	1
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
24	53	14	NA	2
25	65	18	17	7
26	47	18	NA	4
27	46	20	15	4
28	34	6	NA	4
29	61	23	8	1
30	47	26	18	5
31	65	19	NA	4
32	37	14	NA	5
33	48	14	NA	6
34	41	22	24	6
35	41	14	NA	3
36	41	18	21	6
37	42	9	NA	1
38	33	24	NA	4
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
43	43	20	NA	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
51	43	13	NA	6
52	31	15	NA	1
53	45	19	13	3
54	55	24	11	7
55	50	13	NA	7
56	58	26	14	1
57	36	23	9	4
58	45	28	NA	4
59	50	24	NA	1
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
64	36	13	NA	1
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
70	46	29	NA	2
71	58	19	7	1
72	37	22	NA	4
73	46	16	12	5
74	72	24	24	5
75	32	15	NA	6
76	49	24	16	2
77	46	8	NA	6
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
81	53	27	NA	3
82	55	12	NA	4
83	23	15	NA	3
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
88	52	21	NA	4
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
103	46	13	NA	4
104	59	13	NA	1
105	28	28	8	5
106	31	14	NA	4
107	45	29	15	4
108	38	21	NA	7
109	48	25	13	5
110	32	9	NA	5
111	36	27	13	5
112	46	14	NA	5
113	65	24	15	5
114	29	21	8	3
115	34	17	NA	7
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
126	59	13	NA	6
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
143	43	17	NA	7
144	38	21	14	4
145	56	23	10	1
146	34	11	NA	4
147	67	20	NA	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
151	46	12	NA	7
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
159	48	11	NA	5
160	19	12	NA	6
161	64	25	8	2
162	65	12	NA	3
163	46	24	12	4
164	44	17	16	5
165	53	9	NA	7
166	59	16	12	3
167	60	20	21	6
168	28	13	NA	4
169	45	23	NA	2
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
175	55	27	NA	1
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
181	32	15	NA	6
182	51	17	14	4
183	78	28	NA	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
192	57	14	NA	5
193	42	22	19	7
194	37	14	NA	4
195	44	9	NA	1
196	34	19	24	3
197	31	20	NA	6
198	58	26	10	4
199	53	30	7	1
200	33	22	NA	5
201	19	7	NA	3
202	61	13	NA	4
203	42	17	NA	3
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
210	34	23	NA	4
211	49	19	NA	3
212	42	21	NA	6
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
217	34	14	NA	6
218	47	14	NA	5
219	41	19	NA	2
220	33	22	8	3
221	46	13	NA	7
222	25	14	NA	5
223	30	16	7	3
224	41	22	13	3
225	48	8	NA	7
226	42	22	26	4
227	46	20	NA	6
228	51	20	15	4
229	47	20	8	5
230	37	22	NA	1
231	30	21	28	3
232	38	29	NA	4
233	49	30	15	1
234	58	25	7	3
235	47	15	NA	5
236	55	26	NA	4
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
251	38	28	NA	1
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
262	61	19	NA	5
263	47	15	NA	3
264	45	23	NA	3
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
271	20	14	NA	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

id	age	control	depress	stress
1	68	13	NA	5
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
10	31	27	NA	2
11	37	25	21	7
12	48	14	NA	4
13	33	17	20	4
14	47	13	NA	5
15	30	15	NA	1
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
24	53	14	NA	2
25	65	18	17	7
26	47	18	NA	4
27	46	20	15	4
28	34	6	NA	4
29	61	23	8	1
30	47	26	18	5
31	65	19	NA	4
32	37	14	NA	5
33	48	14	NA	6
34	41	22	24	6
35	41	14	NA	3
36	41	18	21	6
37	42	9	NA	1
38	33	24	NA	4
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
43	43	20	NA	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
51	43	13	NA	6
52	31	15	NA	1
53	45	19	13	3
54	55	24	11	7
55	50	13	NA	7
56	58	26	14	1
57	36	23	9	4
58	45	28	NA	4
59	50	24	NA	1
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
64	36	13	NA	1
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
70	46	29	NA	2
71	58	19	7	1
72	37	22	NA	4
73	46	16	12	5
74	72	24	24	5
75	32	15	NA	6
76	49	24	16	2
77	46	8	NA	6
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
81	53	27	NA	3
82	55	12	NA	4
83	23	15	NA	3
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
88	52	21	NA	4
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
103	46	13	NA	4
104	59	13	NA	1
105	28	28	8	5
106	31	14	NA	4
107	45	29	15	4
108	38	21	NA	7
109	48	25	13	5
110	32	9	NA	5
111	36	27	13	5
112	46	14	NA	5
113	65	24	15	5
114	29	21	8	3
115	34	17	NA	7
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
126	59	13	NA	6
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
143	43	17	NA	7
144	38	21	14	4
145	56	23	10	1
146	34	11	NA	4
147	67	20	NA	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
151	46	12	NA	7
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
159	48	11	NA	5
160	19	12	NA	6
161	64	25	8	2
162	65	12	NA	3
163	46	24	12	4
164	44	17	16	5
165	53	9	NA	7
166	59	16	12	3
167	60	20	21	6
168	28	13	NA	4
169	45	23	NA	2
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
175	55	27	NA	1
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
181	32	15	NA	6
182	51	17	14	4
183	78	28	NA	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
192	57	14	NA	5
193	42	22	19	7
194	37	14	NA	4
195	44	9	NA	1
196	34	19	24	3
197	31	20	NA	6
198	58	26	10	4
199	53	30	7	1
200	33	22	NA	5
201	19	7	NA	3
202	61	13	NA	4
203	42	17	NA	3
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
210	34	23	NA	4
211	49	19	NA	3
212	42	21	NA	6
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
217	34	14	NA	6
218	47	14	NA	5
219	41	19	NA	2
220	33	22	8	3
221	46	13	NA	7
222	25	14	NA	5
223	30	16	7	3
224	41	22	13	3
225	48	8	NA	7
226	42	22	26	4
227	46	20	NA	6
228	51	20	15	4
229	47	20	8	5
230	37	22	NA	1
231	30	21	28	3
232	38	29	NA	4
233	49	30	15	1
234	58	25	7	3
235	47	15	NA	5
236	55	26	NA	4
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
251	38	28	NA	1
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
262	61	19	NA	5
263	47	15	NA	3
264	45	23	NA	3
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
271	20	14	NA	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

id	age	control	depress	stress
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
11	37	25	21	7
13	33	17	20	4
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
25	65	18	17	7
27	46	20	15	4
29	61	23	8	1
30	47	26	18	5
34	41	22	24	6
36	41	18	21	6
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
53	45	19	13	3
54	55	24	11	7
56	58	26	14	1
57	36	23	9	4
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
71	58	19	7	1
73	46	16	12	5
74	72	24	24	5
76	49	24	16	2
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
105	28	28	8	5
107	45	29	15	4
109	48	25	13	5
111	36	27	13	5
113	65	24	15	5
114	29	21	8	3
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
144	38	21	14	4
145	56	23	10	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
161	64	25	8	2
163	46	24	12	4
164	44	17	16	5
166	59	16	12	3
167	60	20	21	6
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
182	51	17	14	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
193	42	22	19	7
196	34	19	24	3
198	58	26	10	4
199	53	30	7	1
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
220	33	22	8	3
223	30	16	7	3
224	41	22	13	3
226	42	22	26	4
228	51	20	15	4
229	47	20	8	5
231	30	21	28	3
233	49	30	15	1
234	58	25	7	3
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

id	age	control	depress	stress
1	68	13	NA	5
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
10	31	27	NA	2
11	37	25	21	7
12	48	14	NA	4
13	33	17	20	4
14	47	13	NA	5
15	30	15	NA	1
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
24	53	14	NA	2
25	65	18	17	7
26	47	18	NA	4
27	46	20	15	4
28	34	6	NA	4
29	61	23	8	1
30	47	26	18	5
31	65	19	NA	4
32	37	14	NA	5
33	48	14	NA	6
34	41	22	24	6
35	41	14	NA	3
36	41	18	21	6
37	42	9	NA	1
38	33	24	NA	4
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
43	43	20	NA	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
51	43	13	NA	6
52	31	15	NA	1
53	45	19	13	3
54	55	24	11	7
55	50	13	NA	7
56	58	26	14	1
57	36	23	9	4
58	45	28	NA	4
59	50	24	NA	1
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
64	36	13	NA	1
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
70	46	29	NA	2
71	58	19	7	1
72	37	22	NA	4
73	46	16	12	5
74	72	24	24	5
75	32	15	NA	6
76	49	24	16	2
77	46	8	NA	6
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
81	53	27	NA	3
82	55	12	NA	4
83	23	15	NA	3
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
88	52	21	NA	4
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
103	46	13	NA	4
104	59	13	NA	1
105	28	28	8	5
106	31	14	NA	4
107	45	29	15	4
108	38	21	NA	7
109	48	25	13	5
110	32	9	NA	5
111	36	27	13	5
112	46	14	NA	5
113	65	24	15	5
114	29	21	8	3
115	34	17	NA	7
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
126	59	13	NA	6
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
143	43	17	NA	7
144	38	21	14	4
145	56	23	10	1
146	34	11	NA	4
147	67	20	NA	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
151	46	12	NA	7
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
159	48	11	NA	5
160	19	12	NA	6
161	64	25	8	2
162	65	12	NA	3
163	46	24	12	4
164	44	17	16	5
165	53	9	NA	7
166	59	16	12	3
167	60	20	21	6
168	28	13	NA	4
169	45	23	NA	2
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
175	55	27	NA	1
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
181	32	15	NA	6
182	51	17	14	4
183	78	28	NA	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
192	57	14	NA	5
193	42	22	19	7
194	37	14	NA	4
195	44	9	NA	1
196	34	19	24	3
197	31	20	NA	6
198	58	26	10	4
199	53	30	7	1
200	33	22	NA	5
201	19	7	NA	3
202	61	13	NA	4
203	42	17	NA	3
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
210	34	23	NA	4
211	49	19	NA	3
212	42	21	NA	6
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
217	34	14	NA	6
218	47	14	NA	5
219	41	19	NA	2
220	33	22	8	3
221	46	13	NA	7
222	25	14	NA	5
223	30	16	7	3
224	41	22	13	3
225	48	8	NA	7
226	42	22	26	4
227	46	20	NA	6
228	51	20	15	4
229	47	20	8	5
230	37	22	NA	1
231	30	21	28	3
232	38	29	NA	4
233	49	30	15	1
234	58	25	7	3
235	47	15	NA	5
236	55	26	NA	4
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
251	38	28	NA	1
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
262	61	19	NA	5
263	47	15	NA	3
264	45	23	NA	3
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
271	20	14	NA	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

Missing Data in R

Today

Packages

Missing data mechanisms

Missing data mechanisms

Missing completely at random (MCAR)

Conditionally missing at random (CMAR)

Not missing at random (NMAR)

Data

Chronic pain example

Chronic pain example

Exploratory data analysis (EDA)

EDA

EDA

Missing patterns

Missing patterns

Is it MCAR or MAR?

Is it MCAR or MAR?

Is it MCAR or MAR?

Is it MCAR or MAR?

Testing

Methods for dealing with MCAR

Listwise deletion

Listwise deletion: pros and cons

Casewise (pairwise) deletion

Casewise deletion: pros and cons

Methods for MAR

Unconditional (mean) imputation - Bad

Conditional imputation (regression)

Stochastic Regression

MI

Multiple Imputation

Multiple Imputation

Multiple Imputation

Multiple Imputation

1. Impute with Mice

1. Impute with Mice

PMM

2. Model with Mice

3. Mice Pool Results

3. Mice Pool Results

Plot Imputations

Maximum likelihood (ML)

ML

ML

Chronic pain illustration

Deleting incomplete information

Partial data

Adjusting perceived control

Implicit Imputation

Adjusting Depression Distribution

ML: Cons

Distinguish between NMAR and MAR

Distinguish between NMAR and MAR

Reporting Missing Data

Report

Is it MCAR, MAR, NMAR?

Is it MCAR, MAR, NMAR?

Is it MCAR, MAR, NMAR?

Wrap up

1. Impute with `Mice`

1. Impute with `Mice`

2. Model with `Mice`

3. `Mice` Pool Results

3. `Mice` Pool Results

id	age	control	depress	stress
1	68	13	NA	5
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
10	31	27	NA	2
11	37	25	21	7
12	48	14	NA	4
13	33	17	20	4
14	47	13	NA	5
15	30	15	NA	1
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
24	53	14	NA	2
25	65	18	17	7
26	47	18	NA	4
27	46	20	15	4
28	34	6	NA	4
29	61	23	8	1
30	47	26	18	5
31	65	19	NA	4
32	37	14	NA	5
33	48	14	NA	6
34	41	22	24	6
35	41	14	NA	3
36	41	18	21	6
37	42	9	NA	1
38	33	24	NA	4
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
43	43	20	NA	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
51	43	13	NA	6
52	31	15	NA	1
53	45	19	13	3
54	55	24	11	7
55	50	13	NA	7
56	58	26	14	1
57	36	23	9	4
58	45	28	NA	4
59	50	24	NA	1
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
64	36	13	NA	1
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
70	46	29	NA	2
71	58	19	7	1
72	37	22	NA	4
73	46	16	12	5
74	72	24	24	5
75	32	15	NA	6
76	49	24	16	2
77	46	8	NA	6
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
81	53	27	NA	3
82	55	12	NA	4
83	23	15	NA	3
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
88	52	21	NA	4
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
103	46	13	NA	4
104	59	13	NA	1
105	28	28	8	5
106	31	14	NA	4
107	45	29	15	4
108	38	21	NA	7
109	48	25	13	5
110	32	9	NA	5
111	36	27	13	5
112	46	14	NA	5
113	65	24	15	5
114	29	21	8	3
115	34	17	NA	7
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
126	59	13	NA	6
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
143	43	17	NA	7
144	38	21	14	4
145	56	23	10	1
146	34	11	NA	4
147	67	20	NA	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
151	46	12	NA	7
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
159	48	11	NA	5
160	19	12	NA	6
161	64	25	8	2
162	65	12	NA	3
163	46	24	12	4
164	44	17	16	5
165	53	9	NA	7
166	59	16	12	3
167	60	20	21	6
168	28	13	NA	4
169	45	23	NA	2
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
175	55	27	NA	1
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
181	32	15	NA	6
182	51	17	14	4
183	78	28	NA	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
192	57	14	NA	5
193	42	22	19	7
194	37	14	NA	4
195	44	9	NA	1
196	34	19	24	3
197	31	20	NA	6
198	58	26	10	4
199	53	30	7	1
200	33	22	NA	5
201	19	7	NA	3
202	61	13	NA	4
203	42	17	NA	3
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
210	34	23	NA	4
211	49	19	NA	3
212	42	21	NA	6
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
217	34	14	NA	6
218	47	14	NA	5
219	41	19	NA	2
220	33	22	8	3
221	46	13	NA	7
222	25	14	NA	5
223	30	16	7	3
224	41	22	13	3
225	48	8	NA	7
226	42	22	26	4
227	46	20	NA	6
228	51	20	15	4
229	47	20	8	5
230	37	22	NA	1
231	30	21	28	3
232	38	29	NA	4
233	49	30	15	1
234	58	25	7	3
235	47	15	NA	5
236	55	26	NA	4
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
251	38	28	NA	1
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
262	61	19	NA	5
263	47	15	NA	3
264	45	23	NA	3
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
271	20	14	NA	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

id	age	control	depress	stress
1	68	13	NA	5
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
10	31	27	NA	2
11	37	25	21	7
12	48	14	NA	4
13	33	17	20	4
14	47	13	NA	5
15	30	15	NA	1
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
24	53	14	NA	2
25	65	18	17	7
26	47	18	NA	4
27	46	20	15	4
28	34	6	NA	4
29	61	23	8	1
30	47	26	18	5
31	65	19	NA	4
32	37	14	NA	5
33	48	14	NA	6
34	41	22	24	6
35	41	14	NA	3
36	41	18	21	6
37	42	9	NA	1
38	33	24	NA	4
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
43	43	20	NA	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
51	43	13	NA	6
52	31	15	NA	1
53	45	19	13	3
54	55	24	11	7
55	50	13	NA	7
56	58	26	14	1
57	36	23	9	4
58	45	28	NA	4
59	50	24	NA	1
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
64	36	13	NA	1
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
70	46	29	NA	2
71	58	19	7	1
72	37	22	NA	4
73	46	16	12	5
74	72	24	24	5
75	32	15	NA	6
76	49	24	16	2
77	46	8	NA	6
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
81	53	27	NA	3
82	55	12	NA	4
83	23	15	NA	3
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
88	52	21	NA	4
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
103	46	13	NA	4
104	59	13	NA	1
105	28	28	8	5
106	31	14	NA	4
107	45	29	15	4
108	38	21	NA	7
109	48	25	13	5
110	32	9	NA	5
111	36	27	13	5
112	46	14	NA	5
113	65	24	15	5
114	29	21	8	3
115	34	17	NA	7
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
126	59	13	NA	6
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
143	43	17	NA	7
144	38	21	14	4
145	56	23	10	1
146	34	11	NA	4
147	67	20	NA	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
151	46	12	NA	7
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
159	48	11	NA	5
160	19	12	NA	6
161	64	25	8	2
162	65	12	NA	3
163	46	24	12	4
164	44	17	16	5
165	53	9	NA	7
166	59	16	12	3
167	60	20	21	6
168	28	13	NA	4
169	45	23	NA	2
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
175	55	27	NA	1
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
181	32	15	NA	6
182	51	17	14	4
183	78	28	NA	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
192	57	14	NA	5
193	42	22	19	7
194	37	14	NA	4
195	44	9	NA	1
196	34	19	24	3
197	31	20	NA	6
198	58	26	10	4
199	53	30	7	1
200	33	22	NA	5
201	19	7	NA	3
202	61	13	NA	4
203	42	17	NA	3
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
210	34	23	NA	4
211	49	19	NA	3
212	42	21	NA	6
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
217	34	14	NA	6
218	47	14	NA	5
219	41	19	NA	2
220	33	22	8	3
221	46	13	NA	7
222	25	14	NA	5
223	30	16	7	3
224	41	22	13	3
225	48	8	NA	7
226	42	22	26	4
227	46	20	NA	6
228	51	20	15	4
229	47	20	8	5
230	37	22	NA	1
231	30	21	28	3
232	38	29	NA	4
233	49	30	15	1
234	58	25	7	3
235	47	15	NA	5
236	55	26	NA	4
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
251	38	28	NA	1
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
262	61	19	NA	5
263	47	15	NA	3
264	45	23	NA	3
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
271	20	14	NA	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

id	age	control	depress	stress
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
11	37	25	21	7
13	33	17	20	4
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
25	65	18	17	7
27	46	20	15	4
29	61	23	8	1
30	47	26	18	5
34	41	22	24	6
36	41	18	21	6
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
53	45	19	13	3
54	55	24	11	7
56	58	26	14	1
57	36	23	9	4
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
71	58	19	7	1
73	46	16	12	5
74	72	24	24	5
76	49	24	16	2
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
105	28	28	8	5
107	45	29	15	4
109	48	25	13	5
111	36	27	13	5
113	65	24	15	5
114	29	21	8	3
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
144	38	21	14	4
145	56	23	10	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
161	64	25	8	2
163	46	24	12	4
164	44	17	16	5
166	59	16	12	3
167	60	20	21	6
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
182	51	17	14	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
193	42	22	19	7
196	34	19	24	3
198	58	26	10	4
199	53	30	7	1
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
220	33	22	8	3
223	30	16	7	3
224	41	22	13	3
226	42	22	26	4
228	51	20	15	4
229	47	20	8	5
231	30	21	28	3
233	49	30	15	1
234	58	25	7	3
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4

id	age	control	depress	stress
1	68	13	NA	5
2	38	19	28	7
3	31	20	8	4
4	31	17	28	7
5	58	22	12	3
6	63	26	13	5
7	38	16	23	5
8	54	30	12	1
9	66	20	9	3
10	31	27	NA	2
11	37	25	21	7
12	48	14	NA	4
13	33	17	20	4
14	47	13	NA	5
15	30	15	NA	1
16	48	29	8	3
17	58	27	13	1
18	51	26	9	4
19	47	21	15	2
20	41	17	18	5
21	31	18	26	7
22	52	23	18	3
23	51	22	15	4
24	53	14	NA	2
25	65	18	17	7
26	47	18	NA	4
27	46	20	15	4
28	34	6	NA	4
29	61	23	8	1
30	47	26	18	5
31	65	19	NA	4
32	37	14	NA	5
33	48	14	NA	6
34	41	22	24	6
35	41	14	NA	3
36	41	18	21	6
37	42	9	NA	1
38	33	24	NA	4
39	72	25	9	4
40	54	22	10	3
41	54	26	14	2
42	49	23	8	1
43	43	20	NA	1
44	40	20	16	2
45	46	26	14	2
46	35	25	10	6
47	44	16	17	6
48	41	30	7	1
49	30	20	28	7
50	31	25	19	4
51	43	13	NA	6
52	31	15	NA	1
53	45	19	13	3
54	55	24	11	7
55	50	13	NA	7
56	58	26	14	1
57	36	23	9	4
58	45	28	NA	4
59	50	24	NA	1
60	32	30	11	7
61	51	21	8	2
62	32	16	16	7
63	54	23	12	4
64	36	13	NA	1
65	41	17	24	4
66	52	27	7	2
67	61	27	13	7
68	38	17	16	3
69	38	18	25	4
70	46	29	NA	2
71	58	19	7	1
72	37	22	NA	4
73	46	16	12	5
74	72	24	24	5
75	32	15	NA	6
76	49	24	16	2
77	46	8	NA	6
78	38	26	8	4
79	40	18	27	6
80	40	20	11	4
81	53	27	NA	3
82	55	12	NA	4
83	23	15	NA	3
84	47	22	8	1
85	49	22	28	6
86	62	24	27	6
87	50	18	15	7
88	52	21	NA	4
89	26	18	24	7
90	46	18	25	4
91	45	23	22	6
92	70	28	9	6
93	26	22	11	5
94	26	21	17	4
95	53	16	19	6
96	43	27	15	4
97	22	22	27	4
98	35	19	14	3
99	41	17	17	4
100	48	16	26	7
101	62	25	14	2
102	53	22	13	4
103	46	13	NA	4
104	59	13	NA	1
105	28	28	8	5
106	31	14	NA	4
107	45	29	15	4
108	38	21	NA	7
109	48	25	13	5
110	32	9	NA	5
111	36	27	13	5
112	46	14	NA	5
113	65	24	15	5
114	29	21	8	3
115	34	17	NA	7
116	42	21	20	7
117	39	17	14	4
118	53	22	13	4
119	43	23	13	5
120	43	23	8	3
121	36	20	20	6
122	40	19	20	4
123	67	29	20	6
124	45	29	15	5
125	28	19	13	5
126	59	13	NA	6
127	33	22	16	3
128	28	25	26	5
129	62	22	8	4
130	30	23	9	3
131	37	21	7	1
132	41	22	7	2
133	47	20	9	1
134	56	23	14	4
135	50	16	27	7
136	57	20	16	3
137	51	29	8	1
138	28	20	27	6
139	45	17	8	3
140	34	22	15	5
141	44	29	8	1
142	37	19	15	3
143	43	17	NA	7
144	38	21	14	4
145	56	23	10	1
146	34	11	NA	4
147	67	20	NA	1
148	67	28	15	6
149	46	30	8	5
150	48	17	27	5
151	46	12	NA	7
152	43	25	7	1
153	41	21	22	4
154	41	21	8	2
155	51	29	7	2
156	49	16	17	5
157	26	16	12	4
158	38	24	9	4
159	48	11	NA	5
160	19	12	NA	6
161	64	25	8	2
162	65	12	NA	3
163	46	24	12	4
164	44	17	16	5
165	53	9	NA	7
166	59	16	12	3
167	60	20	21	6
168	28	13	NA	4
169	45	23	NA	2
170	55	25	9	1
171	49	30	27	2
172	53	20	13	2
173	37	30	8	1
174	51	20	19	4
175	55	27	NA	1
176	63	21	9	5
177	48	30	7	4
178	58	28	9	1
179	57	17	13	6
180	49	25	12	3
181	32	15	NA	6
182	51	17	14	4
183	78	28	NA	4
184	56	22	10	6
185	46	18	12	3
186	40	20	22	4
187	55	26	10	2
188	30	16	21	3
189	54	24	8	3
190	55	27	8	1
191	42	29	10	3
192	57	14	NA	5
193	42	22	19	7
194	37	14	NA	4
195	44	9	NA	1
196	34	19	24	3
197	31	20	NA	6
198	58	26	10	4
199	53	30	7	1
200	33	22	NA	5
201	19	7	NA	3
202	61	13	NA	4
203	42	17	NA	3
204	40	18	7	1
205	42	18	22	5
206	36	21	10	2
207	58	19	8	1
208	40	21	12	4
209	68	25	14	5
210	34	23	NA	4
211	49	19	NA	3
212	42	21	NA	6
213	41	27	20	4
214	32	27	12	3
215	50	16	19	5
216	31	17	18	5
217	34	14	NA	6
218	47	14	NA	5
219	41	19	NA	2
220	33	22	8	3
221	46	13	NA	7
222	25	14	NA	5
223	30	16	7	3
224	41	22	13	3
225	48	8	NA	7
226	42	22	26	4
227	46	20	NA	6
228	51	20	15	4
229	47	20	8	5
230	37	22	NA	1
231	30	21	28	3
232	38	29	NA	4
233	49	30	15	1
234	58	25	7	3
235	47	15	NA	5
236	55	26	NA	4
237	54	22	19	6
238	58	17	9	1
239	49	27	14	1
240	57	21	13	5
241	46	27	7	5
242	40	25	9	3
243	29	28	7	3
244	53	23	12	4
245	41	16	13	5
246	31	20	14	3
247	48	21	11	4
248	43	21	10	1
249	66	17	21	2
250	40	20	9	4
251	38	28	NA	1
252	41	27	24	4
253	63	19	13	4
254	42	27	8	4
255	58	20	21	7
256	52	28	20	6
257	51	27	9	6
258	58	28	9	1
259	69	28	15	4
260	41	20	20	4
261	37	25	11	6
262	61	19	NA	5
263	47	15	NA	3
264	45	23	NA	3
265	45	21	7	3
266	47	18	8	3
267	57	20	14	3
268	60	21	10	4
269	50	20	18	6
270	36	25	10	4
271	20	14	NA	4
272	74	28	7	1
273	50	22	10	1
274	61	29	8	2
275	53	24	13	4