Beta Regression in R
Princeton University
2024-03-31
Today
Beta regression
- The beta distribution
- Shapes, mean, and precision
- The beta distribution
Running a beta regression in R
- Example: reading accuracy, dyslexia, and IQ
Other beta models
ZOIB
Ordered beta
Package
The beta distribution
- Rates, proportions, and percentages
- Continuous distribution for 0 < y < 1
- Important: Not including 0 or 1!
- Continuous distribution for 0 < y < 1
- Two parameters:
- Shape 1 and Shape 2
- Controls location, spread, skew
- Shape 1 and Shape 2
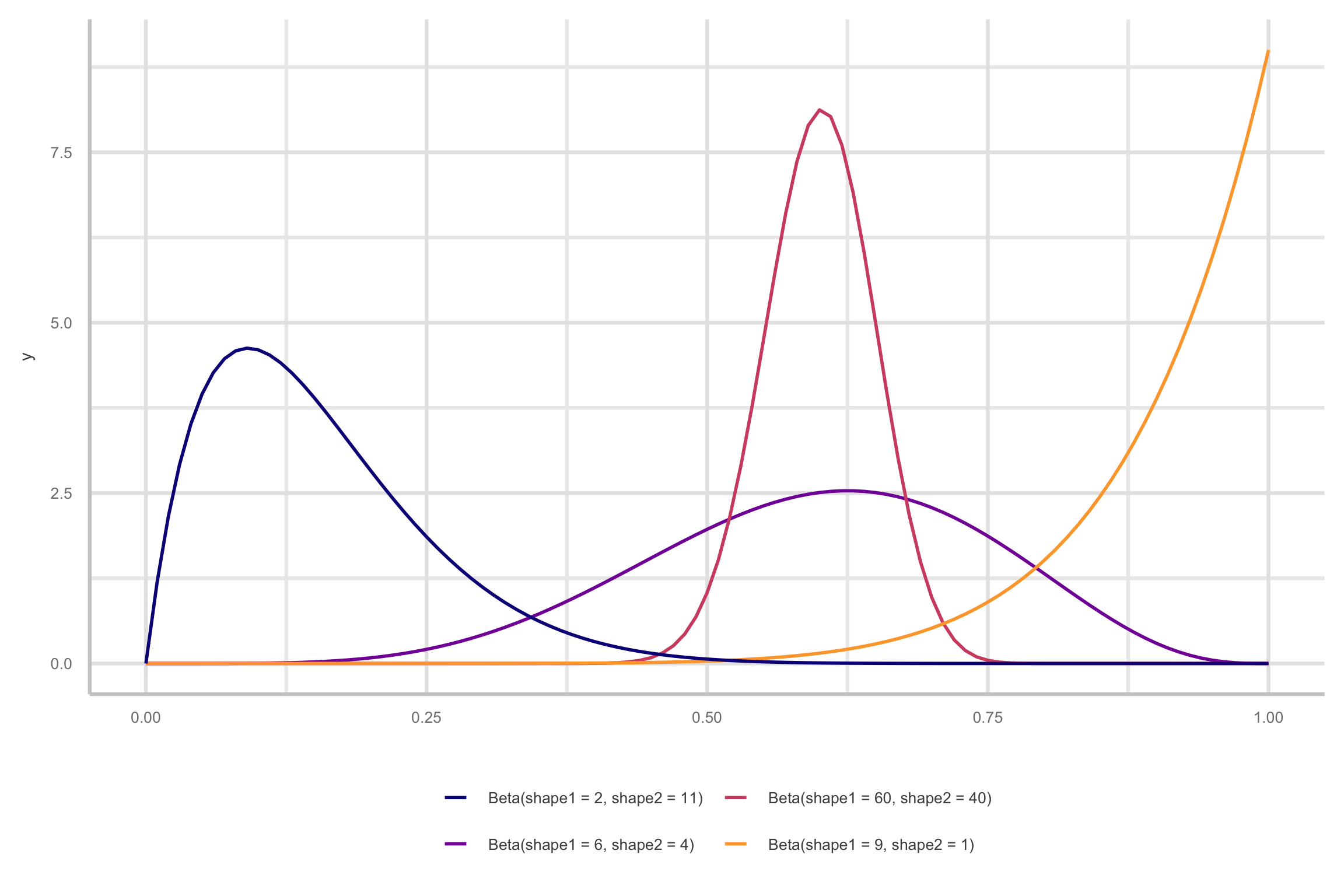
Understanding the shape parameters
Let’s say that there’s an exam worth 10 points where most people score a 6/10
\[ \frac{\text{Number correct}}{\text{Number correct} + \text{Number incorrect}} \]
\[ \frac{6}{6+4} = \frac{6}{10} \]
\[ \frac{a}{a + b} \]
Shape 1 (a)
Shape 2 (b)
Shape parameter
\(\mu\) and \(\phi\)
- \(\mu\) (mean) and \(\phi\) (precision)
\[ \begin{equation} \begin{aligned}[t] \text{Shape 1:} && a &= \mu \phi \\ \text{Shape 2:} && b &= (1 - \mu) \phi \end{aligned} \qquad\qquad\qquad \begin{aligned}[t] \text{Mean:} && \mu &= \frac{a}{a + b} \\ \text{Precision:} && \phi &= a + b \end{aligned} \end{equation} \] Variance = \[ \mu \cdot (1 - \mu)/ (1 + \phi)\]
- Higher \(\phi\) lower variance (narrower distribution)
- Lower \(\phi\) higher variance (wider distribution)
Beta Regression
Beta regression
- Here were are going to use the
betaregpackage to run frequentist version.
Data
From Smithson & Verkuilen (2006) (taken from
betaregpackage)44 Australian primary school children
Dependent variable
accuracy: Score of test for reading accuracy
IVs:
dyslexia: (yes/no; 0.5. -0.5)iqscore: nonverbal IQ (z-scored)
Data
- Load in data from the
betaregpackage
- Contrast code the
dyslexiavariable
Regular LM
model_lm <- lm(accuracy ~ dyslexia*iq,
data = ReadingSkills)
model_parameters(model_lm) %>%
print_md()| Parameter | Coefficient | SE | 95% CI | t(40) | p |
|---|---|---|---|---|---|
| (Intercept) | 0.73 | 0.02 | (0.70, 0.77) | 39.36 | < .001 |
| dyslexia | -0.28 | 0.04 | (-0.35, -0.20) | -7.38 | < .001 |
| iq | 0.02 | 0.02 | (-0.02, 0.06) | 1.13 | 0.266 |
| dyslexia × iq | -0.07 | 0.04 | (-0.15, 4.13e-03) | -1.91 | 0.063 |
Regular LM
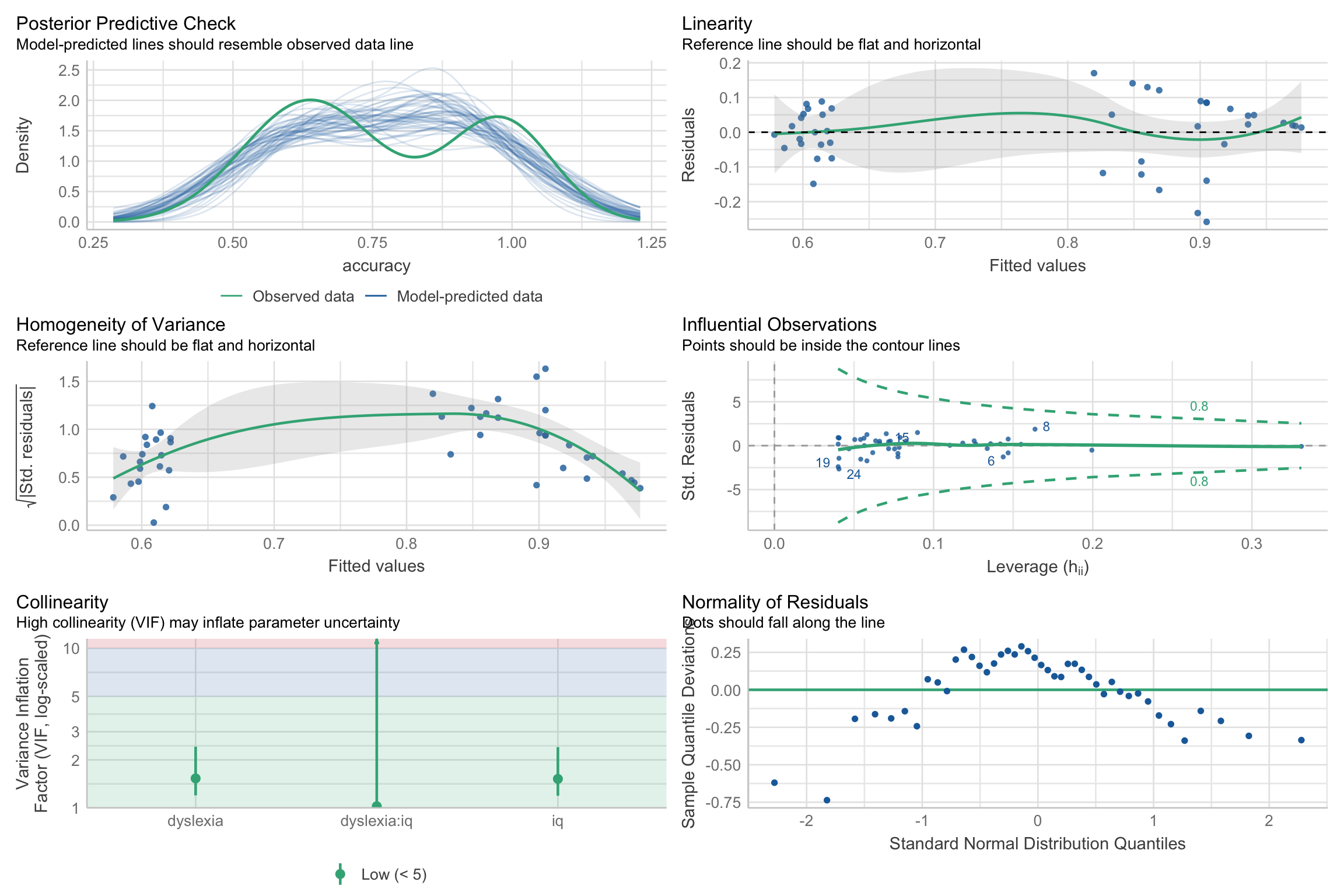
Regular LM
Models using proportions or probabilities:
Asymmetry
Heteoroscadacity
Beta Regression
- To the rescue!
\[ accuracy_i \sim \text{Beta}(\mu_i, \phi) \]
Model has two parts
\(\mu\)
\(\phi\)
\[logit(\mu)= \beta_0 + \beta_1 \text{iq}_i + \beta_2 \text{dyslexia}_i + \beta_3 \text{dyslexia}_i*\text{iq}_i\]
We use the logit link so \(\mu\) is between [0,1]
Beta Regression
- We model precision for each variable by inserting variables after the
|
Interpretation
\(\mu\) parameters are on logit scale
- Can interpret like a logistic regression
| Parameter | Coefficient | SE | 95% CI | z | p |
|---|---|---|---|---|---|
| (Intercept) | 1.12 | 0.14 | (0.84, 1.40) | 7.86 | < .001 |
| dyslexia | -1.48 | 0.29 | (-2.04, -0.92) | -5.20 | < .001 |
| iq | 0.49 | 0.13 | (0.23, 0.75) | 3.65 | < .001 |
| dyslexia × iq | -1.16 | 0.27 | (-1.68, -0.64) | -4.38 | < .001 |
Interpretation
- \(\phi\) (precision) parameter is on log scale so we can exp to get back to original metric
Marginal effects
- Because means are on logit scale we can do what we did with logistic regression and evaluate probabilities
Marginal effects
| term | contrast | estimate | std.error | statistic | p.value | s.value | conf.low | conf.high |
|---|---|---|---|---|---|---|---|---|
| dyslexia | +1 | -0.2450026 | 0.0524356 | -4.672451 | 0.0000030 | 18.358064 | -0.3477744 | -0.1422308 |
| iq | +1 | 0.0274402 | 0.0130397 | 2.104362 | 0.0353469 | 4.822273 | 0.0018829 | 0.0529975 |
Note
For 1-unit increase in
iqthere is an increase of 2 percentage points on reading accuracyDyslexia decreases reading accuracy by 25 percentage points
Model comparison
- LRT
LRT
Interaction
- Simple slopes analysis comparing AME for
iqat each level ofdyslexiavariable
| term | contrast | dyslexia | estimate | std.error | statistic | p.value | s.value | conf.low | conf.high | predicted_lo | predicted_hi | predicted |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| iq | mean(dY/dX) | -0.5 | 0.0955828 | 0.0347942 | 2.747086 | 0.0060127 | 7.377765 | 0.0273873 | 0.1637782 | 0.9397779 | 0.9397997 | 0.9397888 |
| iq | mean(dY/dX) | 0.5 | -0.0225628 | 0.0115910 | -1.946572 | 0.0515861 | 4.276873 | -0.0452808 | 0.0001552 | 0.5961558 | 0.5961475 | 0.5961517 |
Note
For those with dyslexia, an increase in iq deceases reading accuracy by 2 percentage points, \(b\) = -.02, SE = 0.01, 95% CI [-0.04, .00], p = .051. However, this is not statistically significant. For those without dyslexia, reading accuracy improves by 10 percentage points for 1 unit increase in iq, \(b\) = -.02, SE = 0.01, 95% CI [0.027, .163] p = .006.
Visualization - Interaction
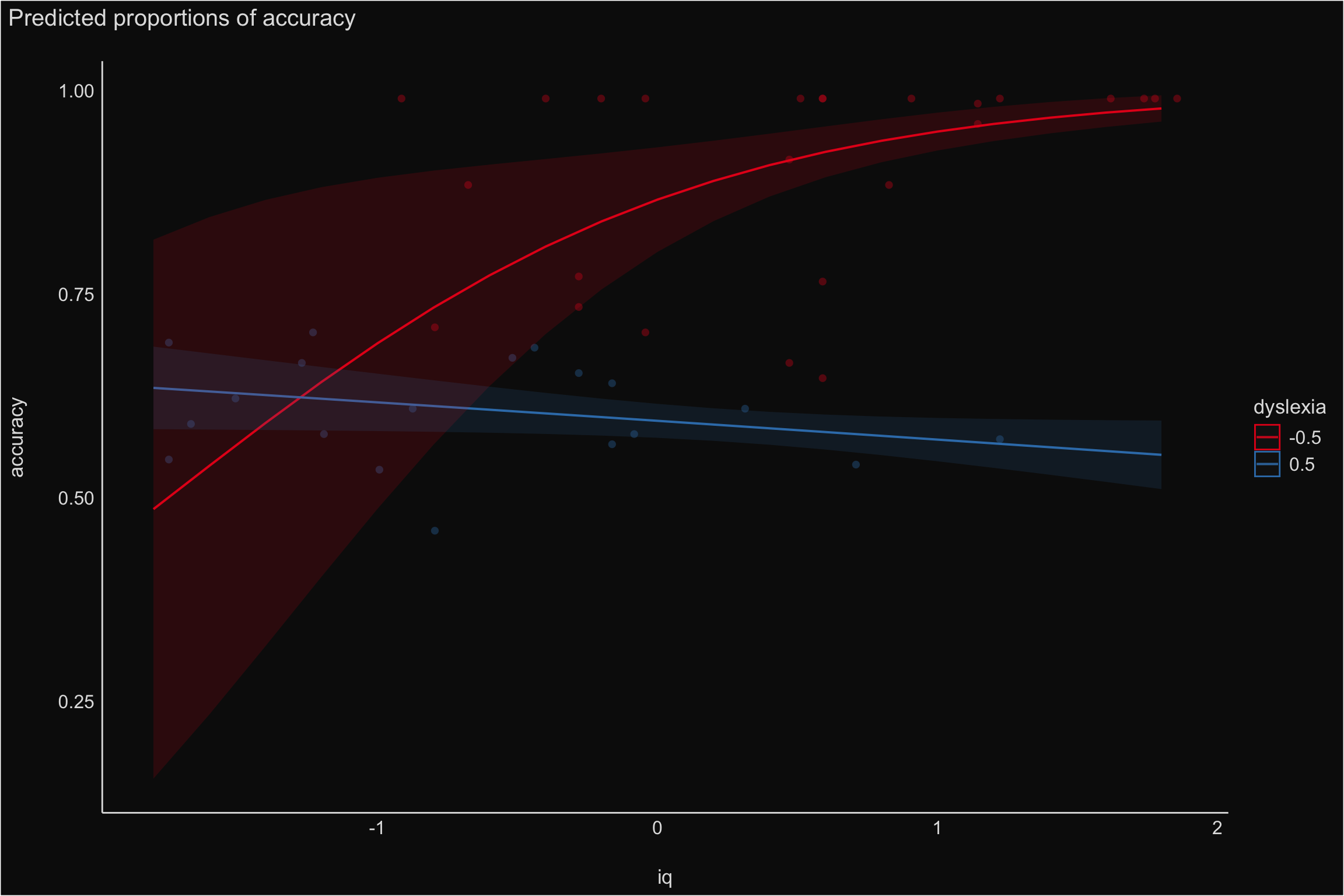
- IQ and Accuracy does not seem to be related to dyslexia
Model Comparisons
- Do we need a precision parameters for each variable?
# before | is mean after is phi/variance
model_beta <- betareg(accuracy ~ dyslexia*iq |dyslexia + iq ,
data = ReadingSkills,
link = "logit")
# estimate only one phi
# before | is mean after is phi/variance
model_beta_nophi <- betareg(accuracy ~ dyslexia*iq ,
data = ReadingSkills,
link = "logit")
test_likelihoodratio(model_beta, model_beta_nophi)# Likelihood-Ratio-Test (LRT) for Model Comparison (ML-estimator)
Name | Model | df | df_diff | Chi2 | p
----------------------------------------------------------
model_beta | betareg | 7 | | |
model_beta_nophi | betareg | 5 | -2 | 29.10 | < .001- \(\phi\) for each variable is warranted
Other beta models
- More complex models like zero-one inflated betas and ordered betas cannot be fit in frequentist framework
ZOIB
- if you have zeros and one in your data
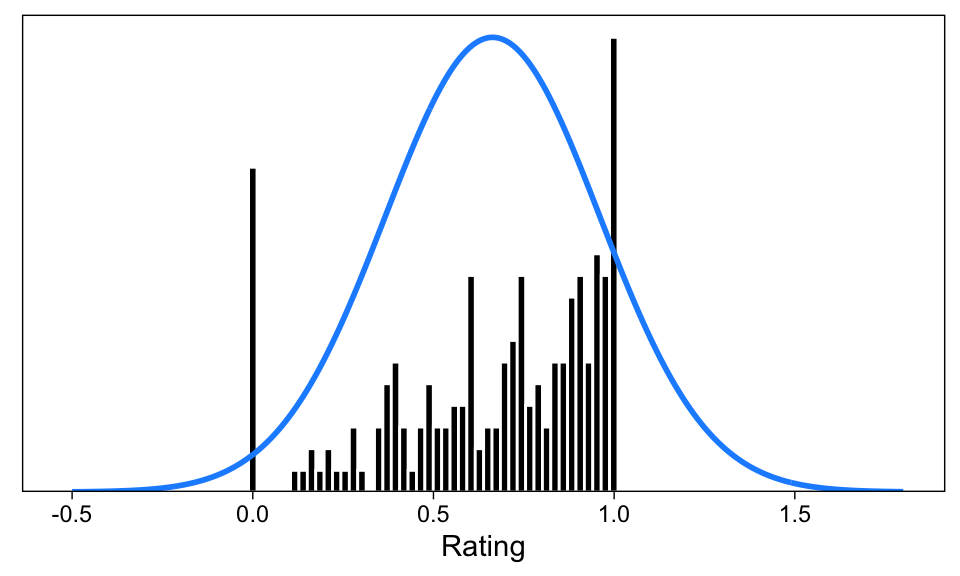
ZOIB
- Three processes
A logistic regression model that predicts if outcome is either (1) 0 or 1 or (2) not exactly 0 or 1 (\(\alpha\) or
zoiin brms)A logistic regression model that predicts if the 0 or 1 outcomes are either (1) 0 or (2) 1 (\(\gamma\) or
coiin brms)A beta regression model that predicts the non-extreme (0 or 1) values) (\(\mu\) and \(\phi\))
brm(
bf(
outcome ~ covariates, # The mean of the 0-1 values, or mu
phi ~ covariates, # The precision of the 0-1 values, or phi
zoi ~ covariates, # The zero-or-one-inflated part, or alpha
coi ~ covariates # The one-inflated part, conditional on the 0s, or gamma
),
data = whatever,
family = zero_one_inflated_beta(),
...
)ZOIB - Output
## Family: zero_one_inflated_beta
## Links: mu = logit; phi = log; zoi = logit; coi = logit
## Formula: Rating ~ group
## phi ~ group
## zoi ~ group
## coi ~ group
## Data: dat (Number of observations: 100)
## Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
## total post-warmup draws = 4000
##
## Population-Level Effects:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept 0.33 0.16 0.03 0.64 1.00 7221 2600
## phi_Intercept 1.50 0.24 1.00 1.94 1.00 6306 3106
## zoi_Intercept -0.80 0.32 -1.44 -0.18 1.00 7341 2983
## coi_Intercept 0.62 0.56 -0.40 1.75 1.00 6324 3166
## groupB 0.91 0.21 0.50 1.32 1.00 6770 2984
## phi_groupB 0.48 0.33 -0.15 1.14 1.00 5750 2654
## zoi_groupB 0.08 0.43 -0.75 0.91 1.00 7812 3178
## coi_groupB -0.87 0.75 -2.35 0.52 1.00 6093 2866
##
## Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).Ordered beta
ZOIB can become complex with lots of parameters to estimate!
- Can take a long time to run
Ordered beta regression is a special case of ZOIB
Robert Kubinec developed it
It combines ordinal and beta regression
Ordered beta regression
We can create three ordered categories to use as an outcome variable: (1) exactly 0 (cutzero), (2) somewhere between 0 and 1, and (3) exactly 1 (cutone)
1 and 3 are modeled as with ordinal logits (exactly 0 and exactly 1) and 2 is modeled as a beta logits
We can just interpret this similarly to beta regression while still including zeros and ones
Ordered beta
## Family: ord_beta_reg
## Links: mu = identity; phi = identity; cutzero = identity; cutone = identity
## Formula: province_count ~ issue_arts_and_culture + issue_education + issue_industry_association + issue_economy_and_trade + issue_charity_and_humanitarian + issue_general + issue_health + issue_environment + issue_science_and_technology + local_connect + years_since_law + year_registered_cat
## Data: data (Number of observations: 593)
## Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
## total post-warmup draws = 4000
##
## Population-Level Effects:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept -0.23 0.33 -0.89 0.44 1.00 1039 1305
## issue_arts_and_cultureTRUE 1.31 0.43 0.47 2.16 1.00 1790 2390
## Family Specific Parameters:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## phi 2.19 0.20 1.82 2.62 1.00 3657 2577
## cutzero -1.26 0.13 -1.53 -1.00 1.00 2438 2762
## cutone 0.34 0.07 0.19 0.47 1.00 3377 2878
##
## Draws were sampled using sample(hmc). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).Summary
Beta regression is an excellent choice for modeling percentages, proportions, and ratios
If you have 0s and 1s, alternatives exist
- ZOIB or ordered beta regression (Bayesian framework)
Not a whole lot of examples using these kind of models, but hopefully this gives you a good start!
Fin
PSY 504: Advanced Statistics