I Dont Likert You: Ordinal Regression

Princeton University

Jason Geller, PH.D.(he/him)

2024-02-25

Today

• Ordinal response variables

• Why you shouldn’t use metric models

• Ordinal regression aka proportional odds models aka cumulative odds models

• Application: Applying to graduate school

Packages

library(tidyverse)
library(easystats)
library(marginaleffects)
library(effects)
library(ordinal)
library(ggeffects)
library(emmeans)
library(foreign)
library(car)
library(knitr)
library(patchwork)
library(MASS)

options(scipen=999)

• Follow along here:https://github.com/jgeller112/PSY504-Advanced-Stats-S24/blob/main/slides/Ordinal_Regression/05-ordinal-regression.qmd

Ordinal Response Variables

• In psychology many variables have a natural ordering

  • Grades (e.g., A,B, C)
  • Education level (e.g., BA, MS, Phd)
  • Competitions (e.g., 1st, 2nd, 3rd)
  • Economic Status (e.g., wealthy, poor)

• Most common are Likert scale (“Lick-ert”) items

This is a cat, not a dog?

1. Very likely to be a dog
2. Somewhat likely to be a dog
3. As likely to be cat or dog
4. Somewhat likely to be a cat
5. Very likely to be a cat

Methods for analysis

• Metric models
  • Models that assume outcomes have a continuous distribution, e.g. t-test
  • Overestimate information in data; common & “simple”
• Nonparametric statistics e.g. analyses of signed ranks (R: ?wilcox.test, etc.)
  • Underestimate information in data; don’t scale well
• Ordinal models
  • A zoo of models that treat outcomes appropriately as ordered categories

“Analyzing ordinal data with metric models: What could possibly go wrong?”

• Liddell and Kruschke (2018) surveyed 68 Psychology articles and found that every article used metric models

  • Can lead to false alarms, failures to detect true effects, distorted effect size estimates, and inversions of effects

“Analyzing ordinal data with metric models: What could possibly go wrong?”

• Three main shortcomings of metric models:

  • Response categories may not be (e.g. psychologically) equidistant

“Analyzing ordinal data with metric models: What could possibly go wrong?”

• Response categories may not be (e.g. psychologically) equidistant

• Responses can be non-normally distributed

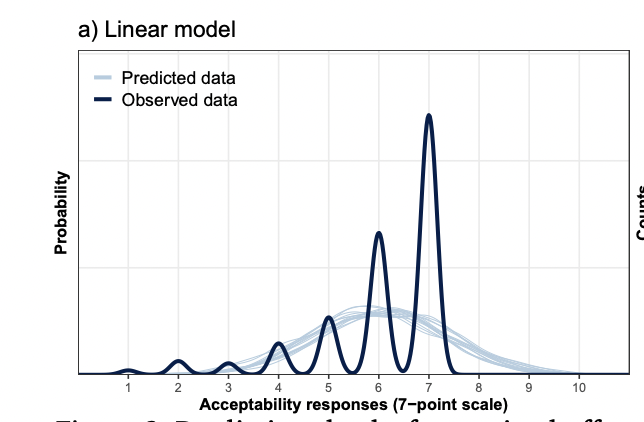
“Analyzing ordinal data with metric models: What could possibly go wrong?”

• Response categories may not be (e.g. psychologically) equidistant

• Responses can be non-normally distributed

• Can treat differences in variances of underlying variable inappropriately

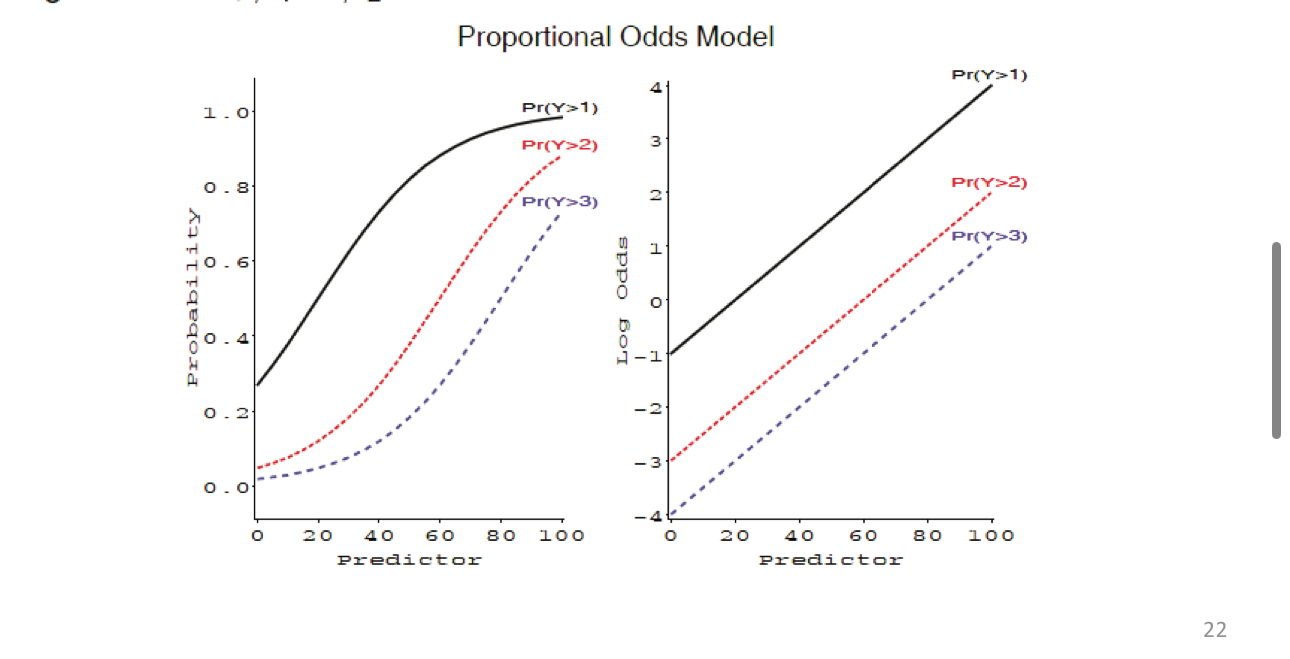
Proportional-Odds Cumulative Logit Model

Cumulative model: Latent variable interpretation

• A simple motivation

  • You have a continuous latent variable \(\tilde{Y}\) that can be be categorized into bins (K thresholds): \(\tau = (\tau_1, \dots, \tau_k)\)

    • Latent Honey’s catness

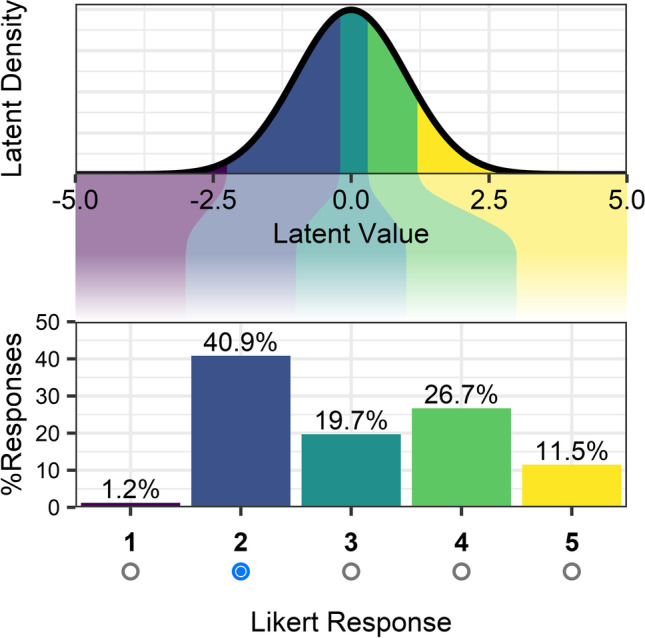
Ordered = Cumulative

• We will use the cumulative distribution to model our ordered categories

• Cumulative probability

  • \(F(x) = P(X \leq x)\)
    • Preserves order

Richard McElreath

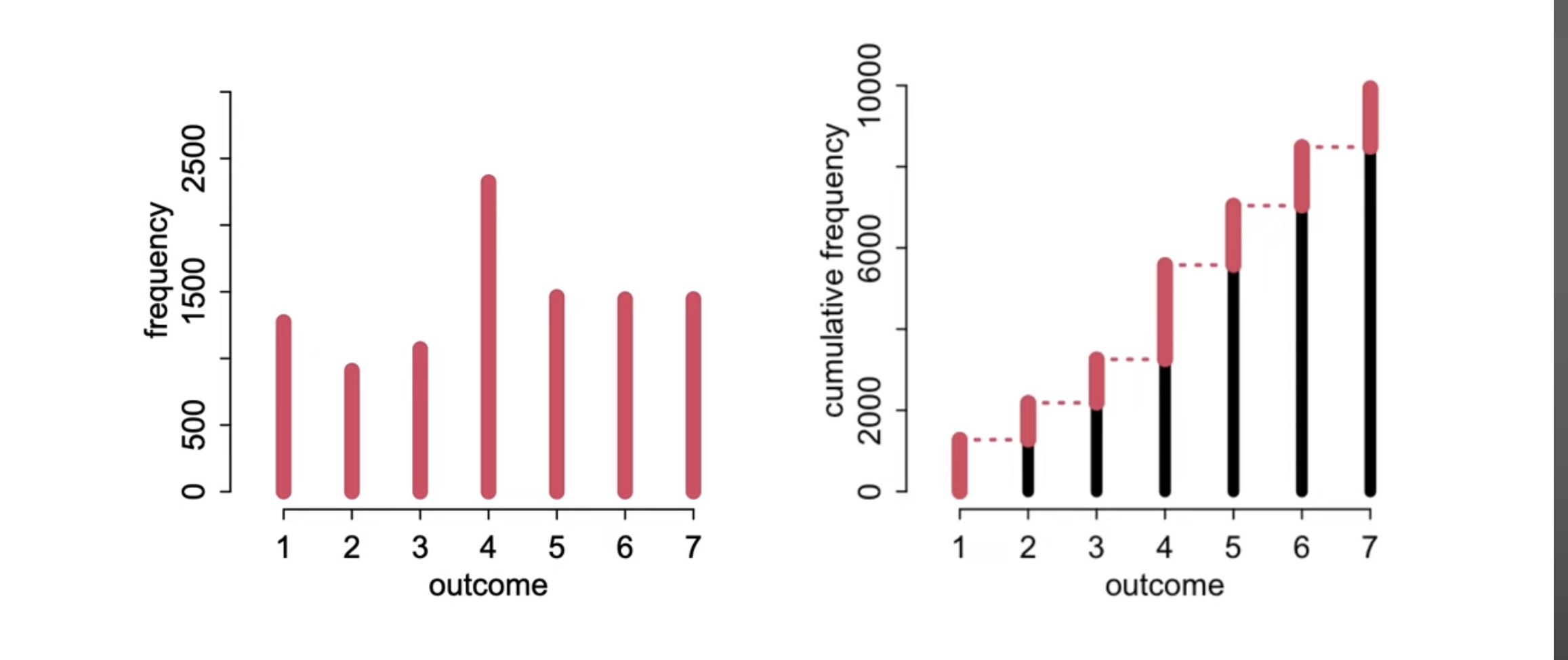
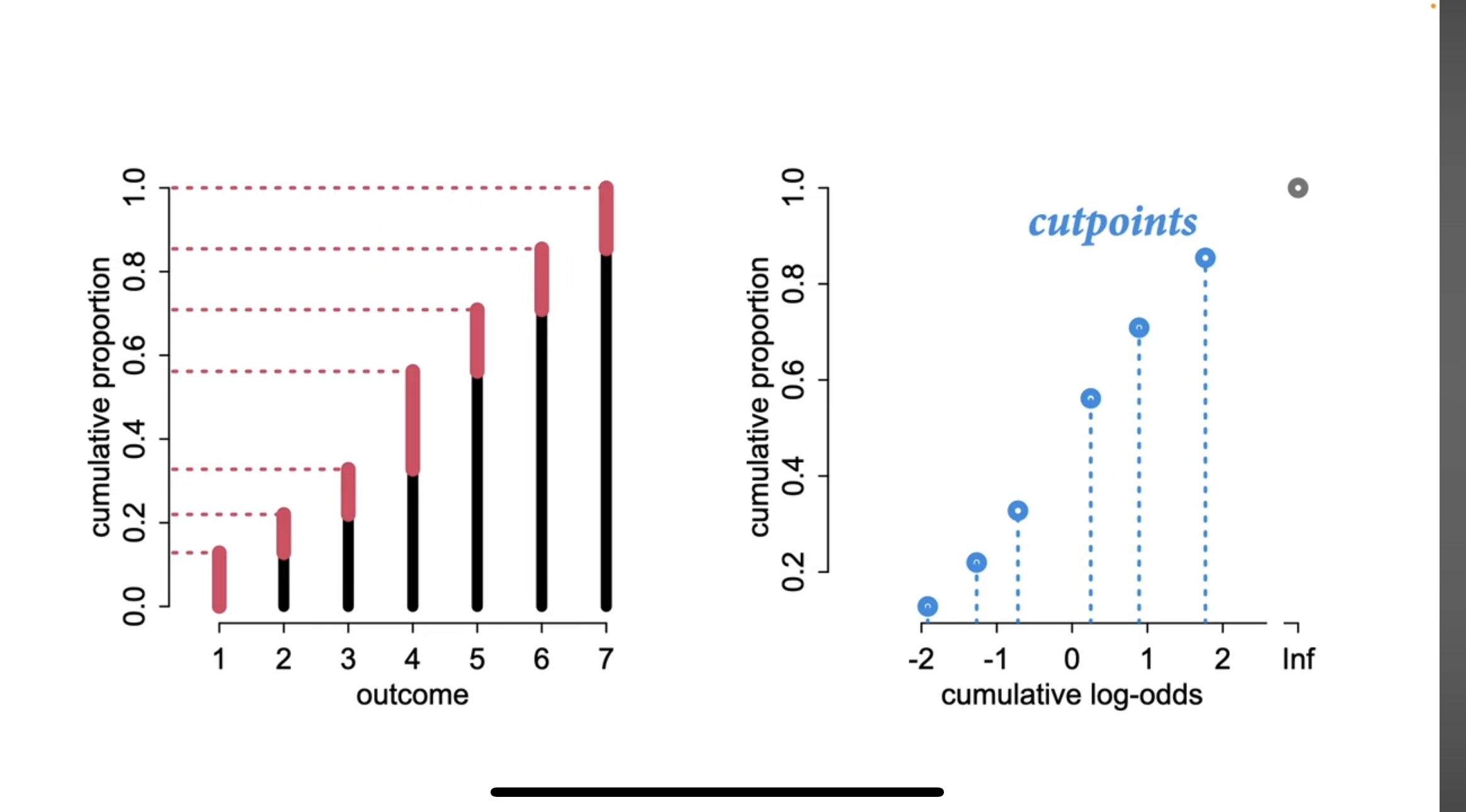
Cumulative logit model

\(P_k\)	Probability of being in category k
\(C_{pk}\)	Cumulative probability of being in category k or lower
1- \(C_{pk}\)	Probability of being above category k

\[\textrm{Odds} = \frac{\# \textrm{successes}}{\# \textrm{failures}}= \frac{\# \textrm{successes}/n}{\# \textrm{failures}/n}= \frac{p}{1-p}\]

• Cumulative Odds of being in at least in category k to below category k to above category k

  \[C_{pk}/1-C_{pk}\]\[log(C_{pk}/1-C_{pk})\]

Cumulative logit model

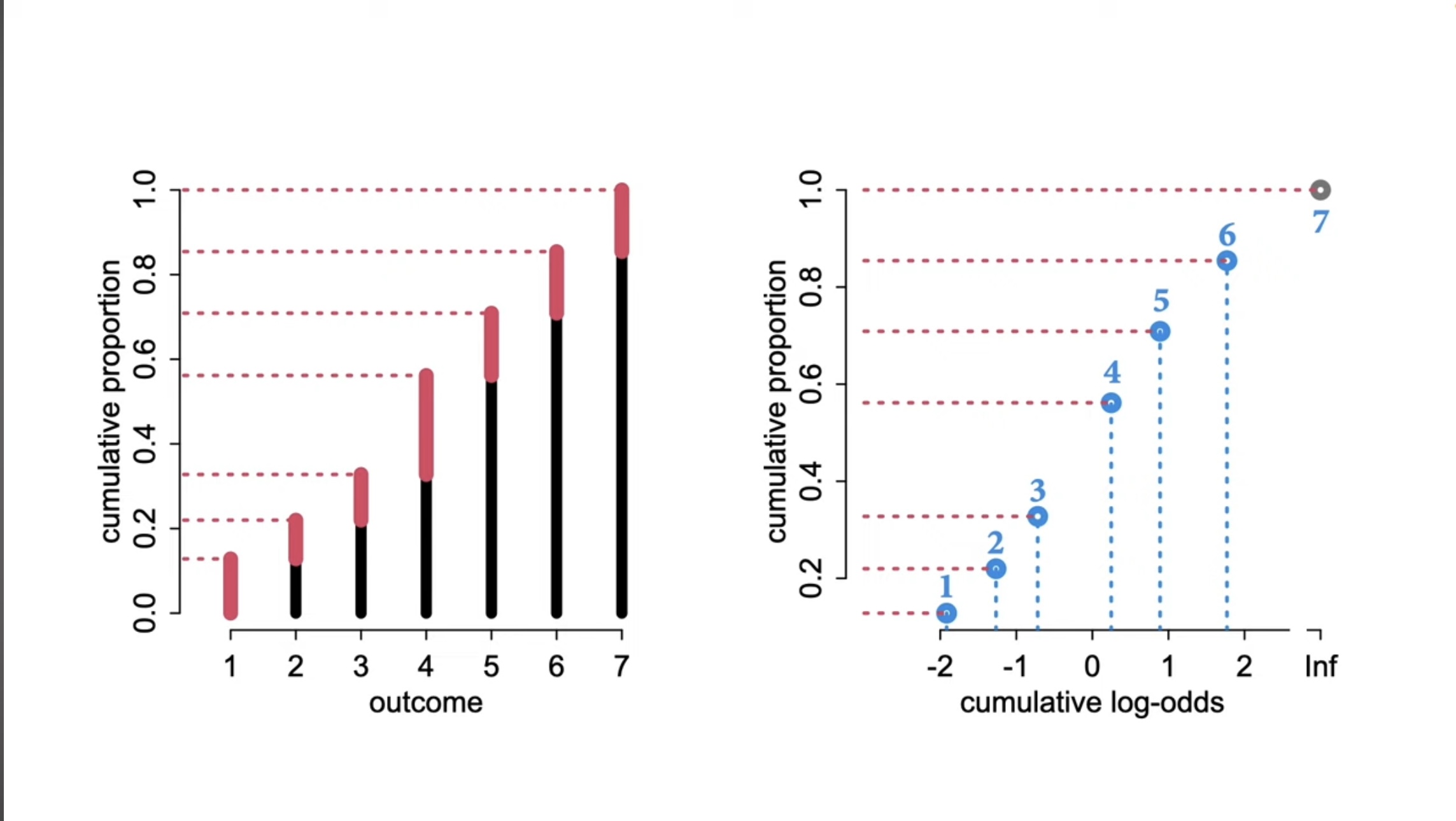
Richard McElreath

Cumulative logit model

Richard McElreath

Cumulative logit model

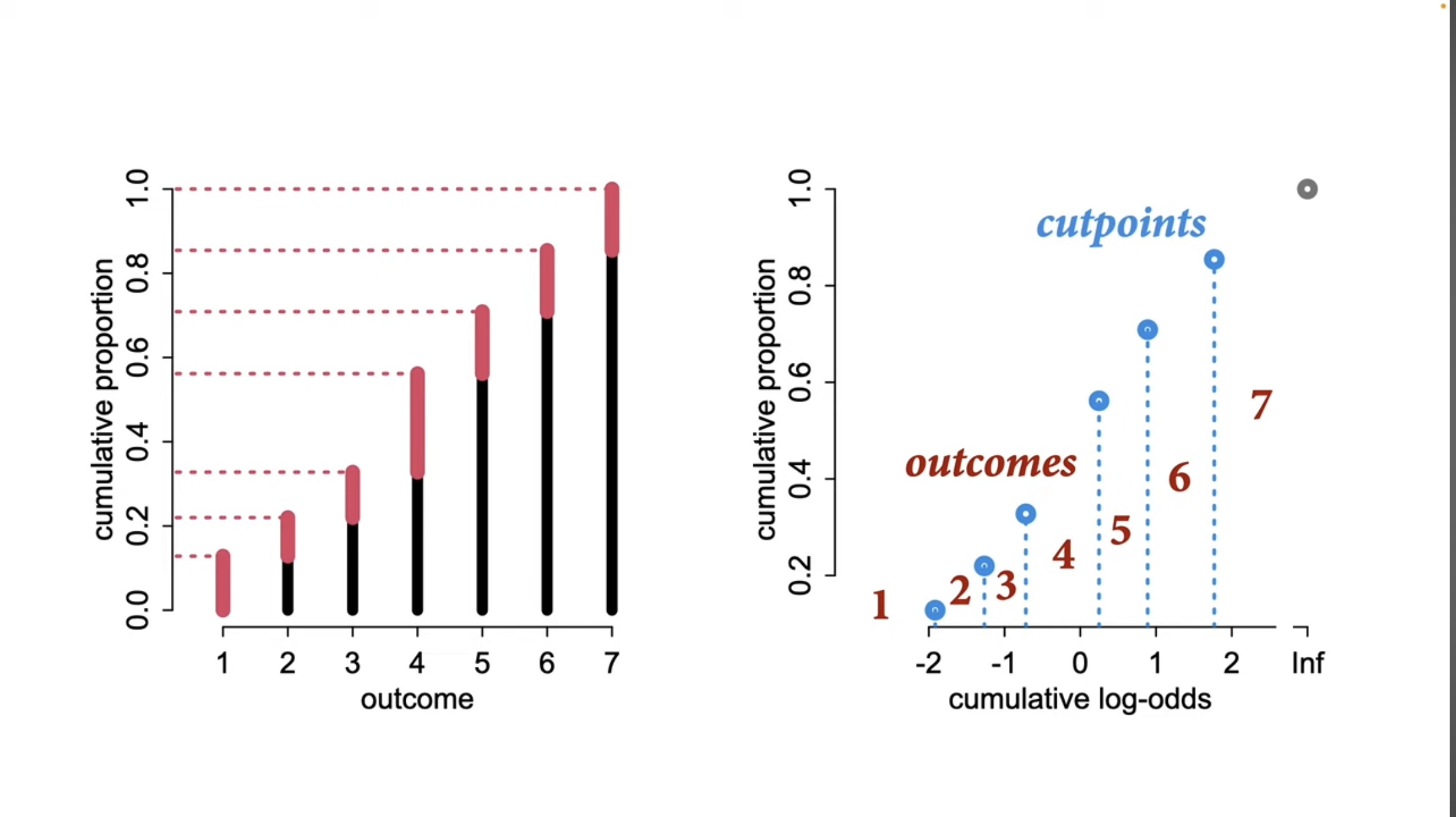
Richard McElreath

Cumulative logit ordinal regression model

\[log (\frac{C_{pk}}{1-C_{pk}}) = \alpha - \beta_{j0}\] \[\begin{array}{rcl} L_1 &=& \alpha_1-\beta_1x_1-\cdots-\beta_p X_p\\ L_2 &=& \alpha_2-\beta_1x_1-\cdots-\beta_p X_p & \\ L_{J-1} &=& \alpha_{J-1}-\beta_1x_1-\cdots-\beta_p X_p \end{array}\]

• Here we are estimating J-1 equations simultaneously

• Each equation as a different intercept \(\alpha_k\) (thresholds/cut points) but a common slope \(\beta\)

• Intercepts are always ordered in size \(\alpha_1\) < \(\alpha_2\)

Cumulative logit ordinal regression model

\[\begin{array}{rcl} L_1 &=& \alpha_1-\beta_1x_1-\cdots-\beta_p X_p\\ L_2 &=& \alpha_2-\beta_1x_1-\cdots-\beta_p X_p& \\ L_{J-1} &=& \alpha_{J-1}-\beta_1x_1-\cdots-\beta_p X_p \end{array}\]

• Where:

  • \(\alpha\) (intercepts/thresholds/cut-offs) = Log-odds of falling into or below category

  • \(\beta\) = Slope (constant between categories)

  • \(-\) = Helps with interpretation (positive \(b\) higher chance of being in higher categories)

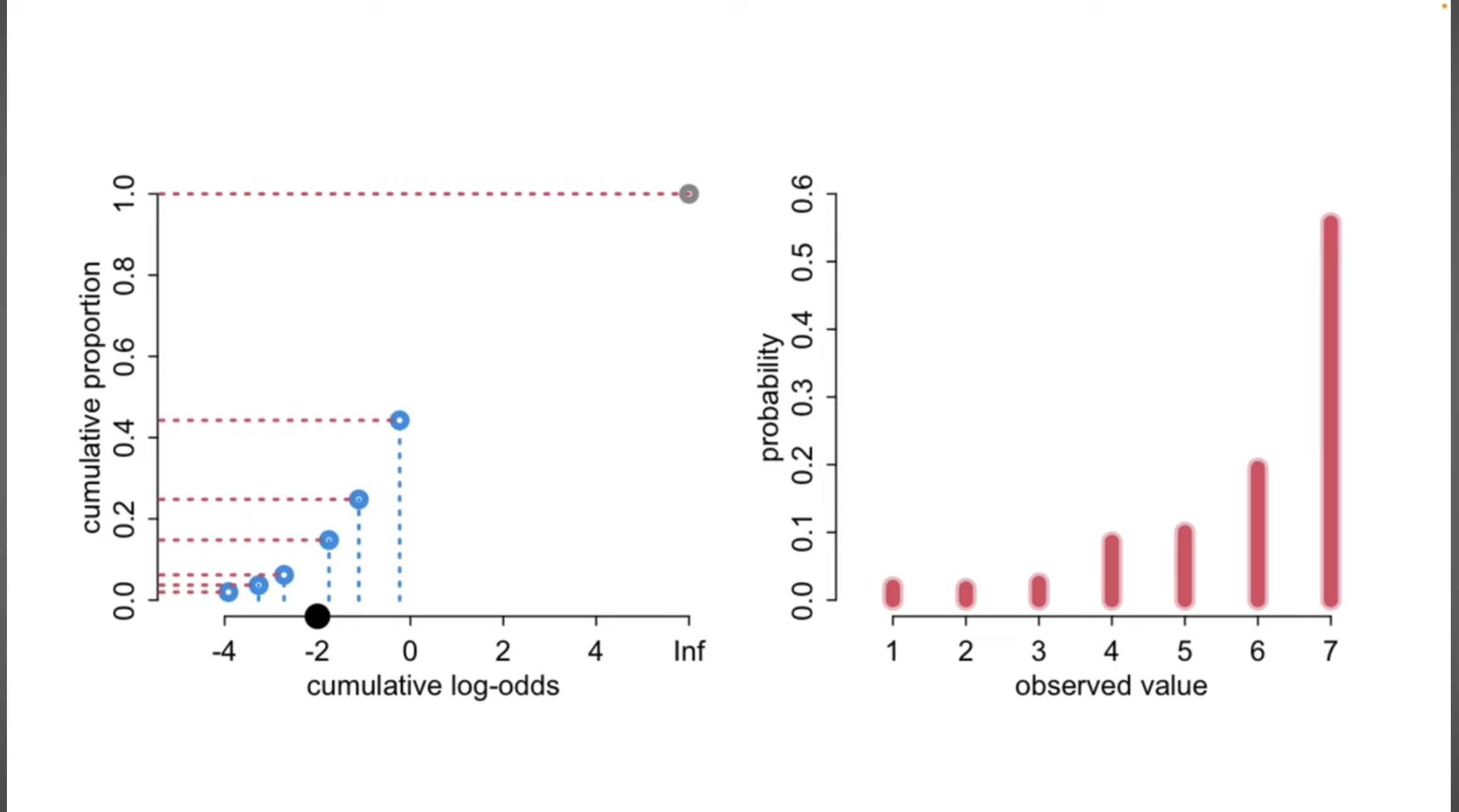
Cumulative logit ordinal regression model

• Normal parametrization (with addition)

• Higer coefs = higher probability of being in lower categories

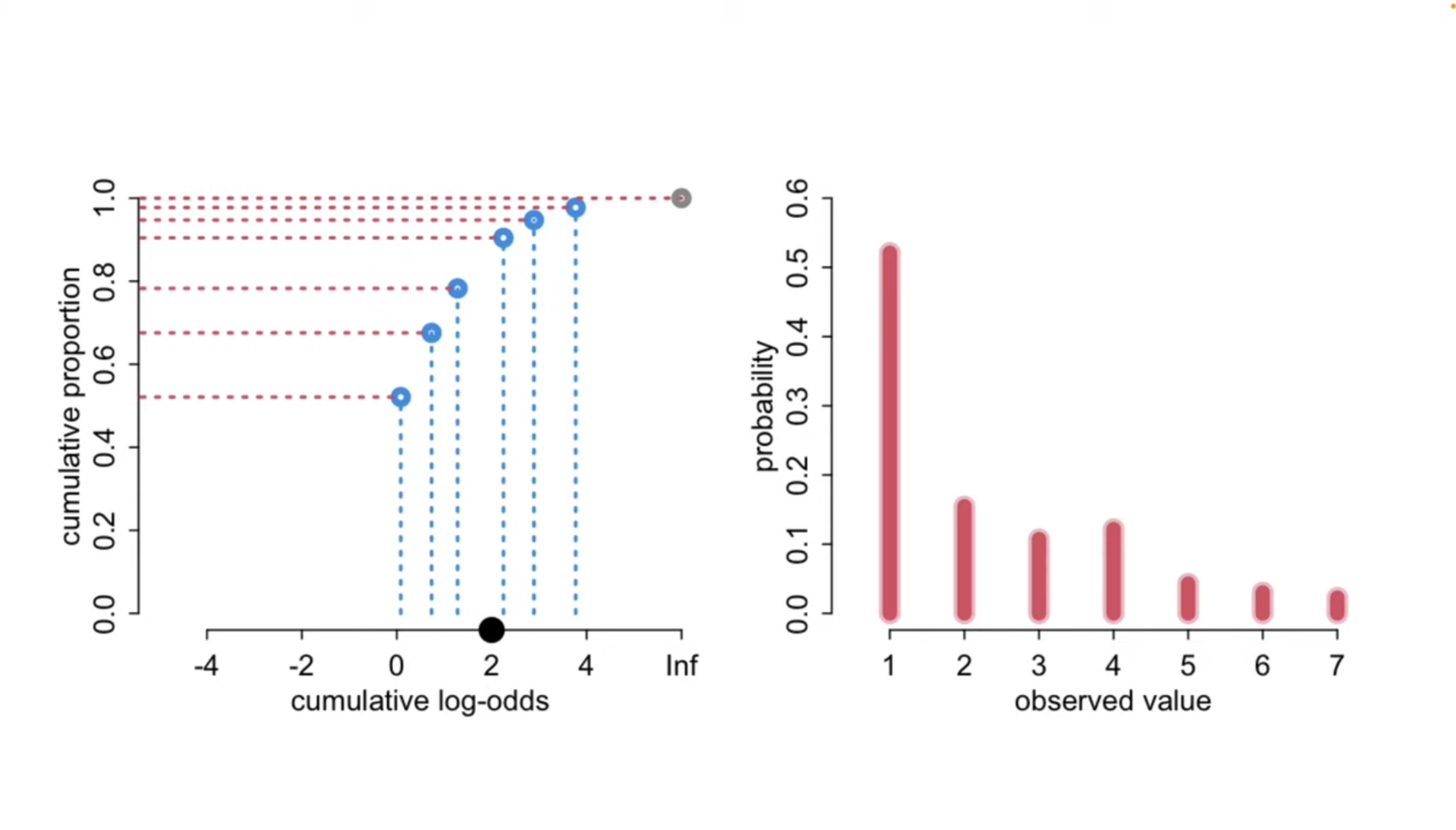
• lower coefs = lower probablity in lower categories

Proportional odds assumption

• Assumes slope is equal between categories
  • Critical for interpretation!

Data: postgraduate school applications

• Undergraduate students report how likely they were to apply to graduate school (apply): “Unlikely”, “Somewhat Likely”, “Very likely”

• Got additional information: GPA (gpa), parent education (pared) (college vs. no college), type of schooling (public) (public vs. private)

apply	n	proportion
somewhat likely	140	0.35
unlikely	220	0.55
very likely	40	0.10

Data: postgraduate school applications

[1] very likely     somewhat likely unlikely        somewhat likely
[5] somewhat likely unlikely       
Levels: unlikely < somewhat likely < very likely

A simple model

\[\text{logit}(p(y_i \leq j)) = \theta_j - \beta_2 \text{parent_education}_i\]

• Fit the model with ordinal::clm can also use MASS:polr

library(ordinal) # clm function

formula: apply ~ pared
data:    dat

 link  threshold nobs logLik  AIC    niter max.grad cond.H 
 logit flexible  400  -361.40 728.79 5(0)  1.25e-10 9.3e+00

Coefficients:
       Estimate Std. Error z value  Pr(>|z|)    
pared1   1.1275     0.2634    4.28 0.0000187 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Threshold coefficients:
                            Estimate Std. Error z value
unlikely|somewhat likely      0.3768     0.1103   3.415
somewhat likely|very likely   2.4519     0.1826  13.430

Interpreting output

• Two parts (2 thresholds and 1 coef) - what’s up with that?

  • Coefficients (slope)
    • Can be interpreted similarly to logistic regression

term	estimate	std.error	statistic	p.value	coef.type
pared1	1.127491	0.2634324	4.280001	0.0000187	location

Interpreting output

term	estimate	std.error	statistic	p.value	coef.type
unlikely|somewhat likely	0.3768424	0.1103421	3.415217	0.0006373	intercept
somewhat likely|very likely	2.4518560	0.1825629	13.430201	0.0000000	intercept

• Thresholds (cut-offs)

  • Less than or equal to a certain level vs greater than that level

• j = 1: log-odds of rating = 1 vs. 2-3 (when x = 0)

• j = 2: log-odds of rating = 1-2 vs. 3 (when x = 0)

Cumulative odds ratios

tidy(ols1, exponentiate=TRUE) %>%
  filter(coef.type=="location") %>%
  kable()

term	estimate	std.error	statistic	p.value	coef.type
pared1	3.087899	0.2634324	4.280001	0.0000187	location

• Sometimes odds ratios are more meaningful

  • Just exp the log cumulative odds!

• Almost 3x more likely to apply to college if parent went to college

Probabilities

\[p(logit)=\frac{e^{logit}}{1+e^{logit}}\frac{exp(a_k - bx)}{1+exp(a_k - bx)}\]

Probabilities

## view a summary of the model
marginaleffects::marginal_means(ols1, variables="pared") %>% kable()

group	term	value	pared	estimate	std.error	statistic	p.value	s.value	conf.low	conf.high
unlikely	pared	0	0	0.5931113	0.0266289	22.273220	0.0000000	362.66373	0.5409196	0.6453030
unlikely	pared	1	1	0.3206800	0.0532744	6.019403	0.0000000	29.08949	0.2162641	0.4250959
somewhat likely	pared	0	0	0.3275858	0.0239325	13.687897	0.0000000	139.25879	0.2806789	0.3744926
somewhat likely	pared	1	1	0.4692270	0.0333495	14.069986	0.0000000	146.94870	0.4038632	0.5345908
very likely	pared	0	0	0.0793029	0.0133296	5.949368	0.0000000	28.46878	0.0531773	0.1054285
very likely	pared	1	1	0.2100930	0.0424965	4.943774	0.0000008	20.31569	0.1268014	0.2933846

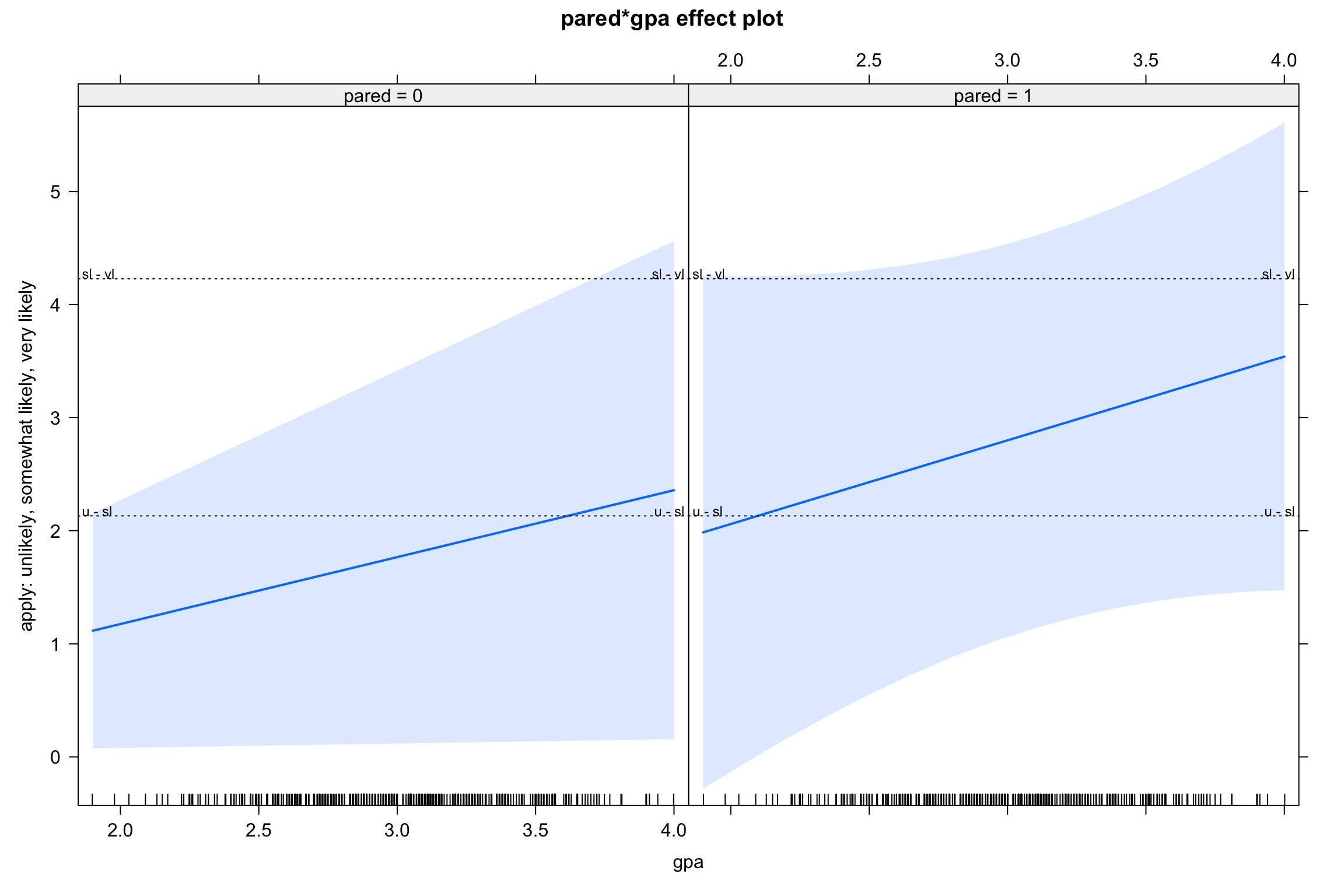
Model visualizations

plot_predictions(ols1, condition = "pared", type = "prob") + facet_wrap(~group) + labs(x = "Parent Education", y = "predicted probability") +  scale_y_continuous(labels = scales::percent) + theme_lucid(base_size=20)

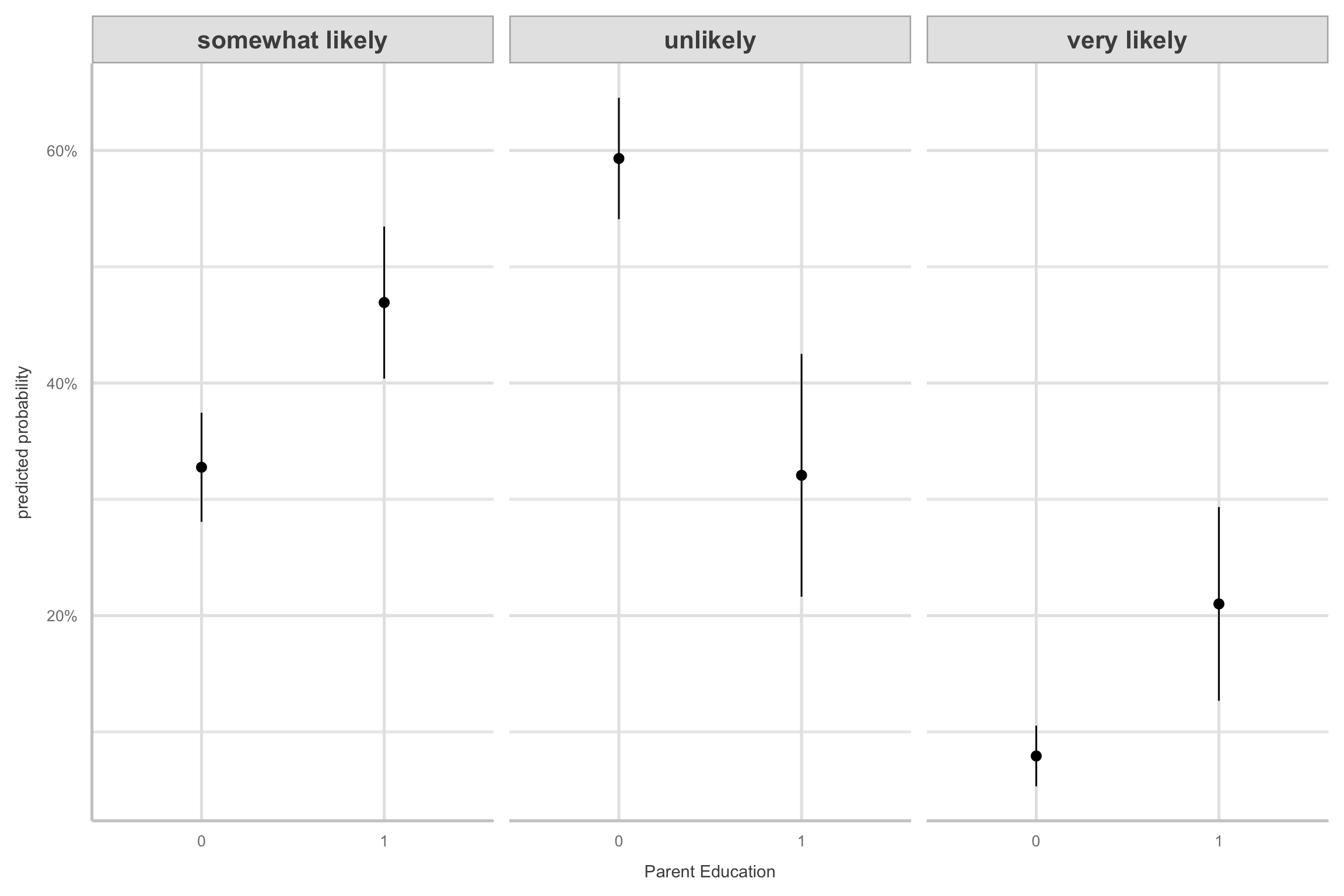
• How could we make the figure better?

Marginal effects

avg_comparisons(ols1) %>%
 kable()

term	group	contrast	estimate	std.error	statistic	p.value	s.value	conf.low	conf.high
pared	somewhat likely	1 - 0	0.1416413	0.0269456	5.256569	0.0000001	22.699959	0.0888289	0.1944536
pared	unlikely	1 - 0	-0.2724313	0.0584070	-4.664363	0.0000031	18.301281	-0.3869069	-0.1579558
pared	very likely	1 - 0	0.1307901	0.0403250	3.243403	0.0011811	9.725639	0.0517546	0.2098255

Testing proportional odds assumption

• brant test

  • Likelihood of the full ordinal logistic regression model (which makes the proportional odds assumption) to the likelihood of a reduced model that does not make this assumption

    • You want a ns \(\chi^2\) test

library(gofcat)# prop odds assum
#need to fit different model

brant.test(ols1)

Brant Test:
           chi-sq   df   pr(>chi)
Omnibus     0.017    1        0.9
pared1      0.017    1        0.9

H0: Proportional odds assumption holds

Test proportional odds assumption

if test is violated, there are a few options:

• Multinomial regression

  • Use lowest level/rank as reference

• Adjacent category model

• Non-proportional odds (NPO) model

Test proportional odds assumption

• In VGAM, the NPO model is fit using family = cumulative(parallel=FALSE)

library(VGAM)
# from textbook 
ols_nom <- VGAM::vglm(apply ~ pared,family=cumulative(parallel = FALSE,  reverse = TRUE), data=dat)

model_parameters(ols_nom) %>%
  kable()

Parameter	Coefficient	SE	CI	CI_low	CI_high	z	df_error	p
(Intercept):1	-0.3783364	0.1109021	0.95	-0.5957005	-0.1609724	-3.411446	Inf	0.0006462
(Intercept):2	-2.4407354	0.2006560	0.95	-2.8340140	-2.0474568	-12.163778	Inf	0.0000000
pared1:1	1.1438043	0.2924980	0.95	0.5705187	1.7170898	3.910469	Inf	0.0000921
pared1:2	1.0936618	0.3703706	0.95	0.3677487	1.8195749	2.952885	Inf	0.0031482

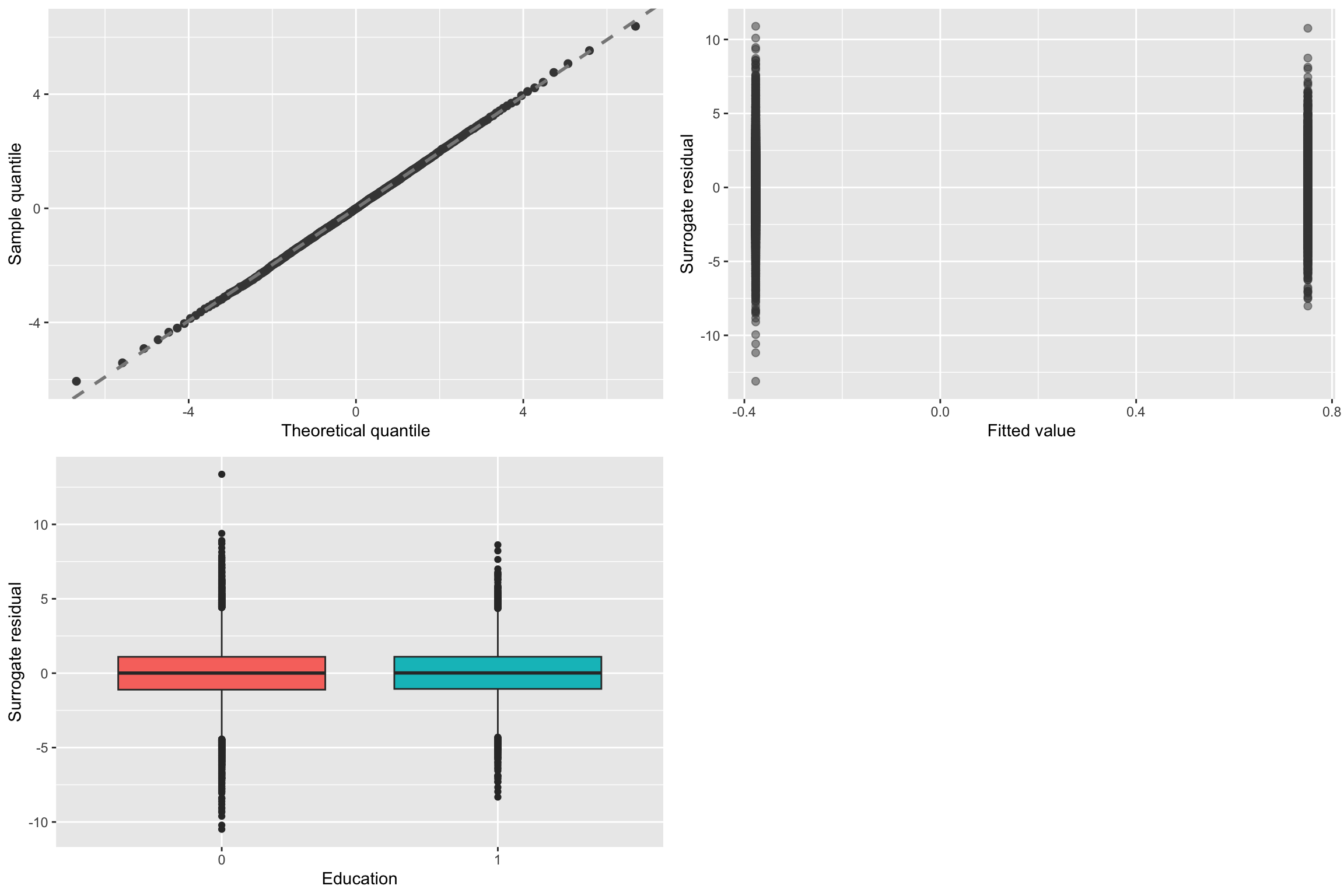
Test ordinal assumptions

• No easystats functions :(

• sure package: surrogate residuals

  • Based on continuous residuals
    • Normality
    • Linearity
    • Homoscedasticity

Note

For multicollinearity look at correlation between variables

Test ordinal assumptions

Model 2: Add Public School + GPA

• Let’s run this model:

ols2 = clm(apply ~ pared + public + gpa, data=dat)

Interpreting Output

• Coefs

Test proportional odds assumption

# test prop odds assumption model 2
brant.test(ols2)

Brant Test:
           chi-sq   df   pr(>chi)  
Omnibus     4.343    3      0.227  
pared1      0.132    1      0.716  
public1     3.443    1      0.064 .
gpa         0.179    1      0.672  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

H0: Proportional odds assumption holds

Visualization: stacked area plots (continuous predictors)

library(effects) # stacked plots

stack <- plot(effect("gpa", ols2), style="stacked")

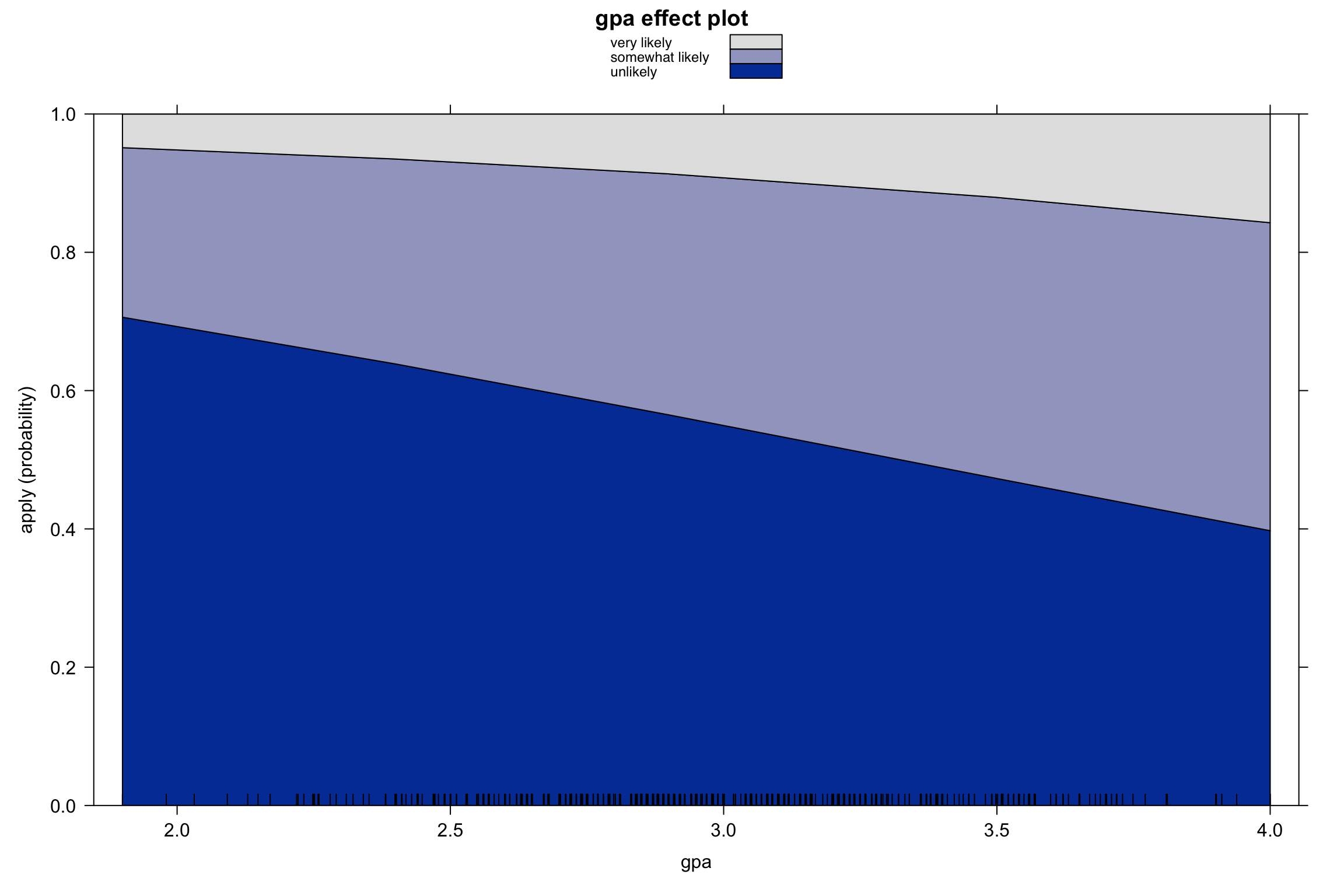
Visualization: stacked area plots (categorical predictors)

library(effects) # stacked plots

stack <- plot(effect("public", ols2), style="stacked")

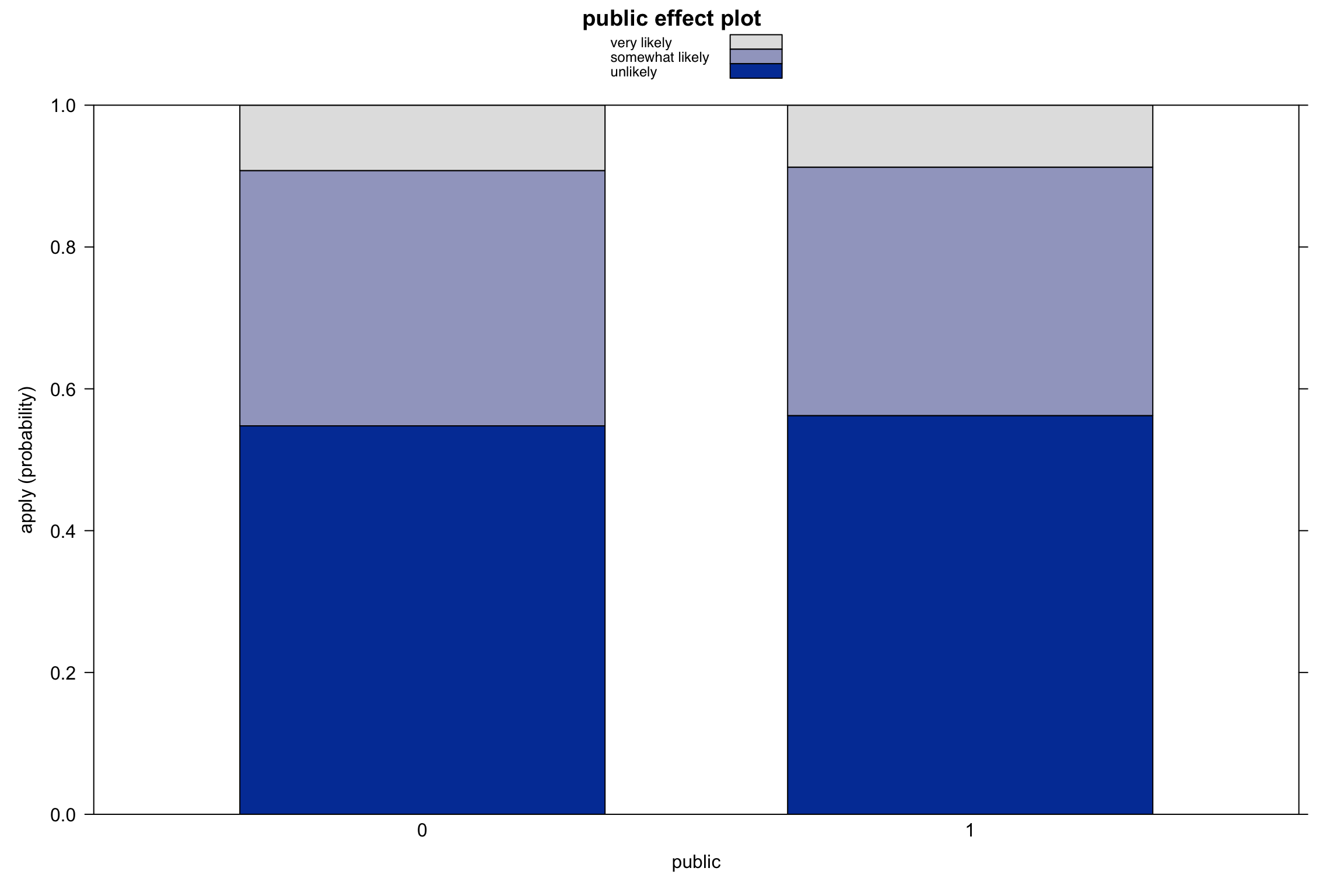
Model 3: Add public school + GPA interaction

term	estimate	std.error	statistic	p.value	coef.type
public1	-0.0621122	0.2984302	-0.2081296	0.8351278	location
pared1	0.5875071	2.1304962	0.2757607	0.7827319	location
gpa	0.5918130	0.2826551	2.0937637	0.0362810	location
pared1:gpa	0.1484331	0.6819411	0.2176627	0.8276920	location

Model Comparisons

• Likelihood ratio tests (LRT)

  • Model comparisons

#main effects model vs. interaction
ols_test <- anova(ols2, ols3)

knitr::kable(ols_test)

	no.par	AIC	logLik	LR.stat	df	Pr(>Chisq)
ols2	5	727.0249	-358.5124	NA	NA	NA
ols3	6	728.9774	-358.4887	0.0474444	1	0.8275715

Testing significance

#main effects model vs. interaction
# USE TYPE III IF INTERACTIONS ARE IMPORTANT
ols_test <- anova(ols3, type="III")
knitr::kable(ols_test)

	Df	Chisq	Pr(>Chisq)
public	1	0.0433179	0.8351278
pared	1	0.0760440	0.7827319
gpa	1	4.3838466	0.0362810
pared:gpa	1	0.0473770	0.8276920

Visualization: Interactions

#interact <- ggemmeans(ols2, terms= c("gpa", "pared"))
plot_predictions(ols3, condition = c("gpa", "pared"), type = "prob")+ facet_grid(~group)

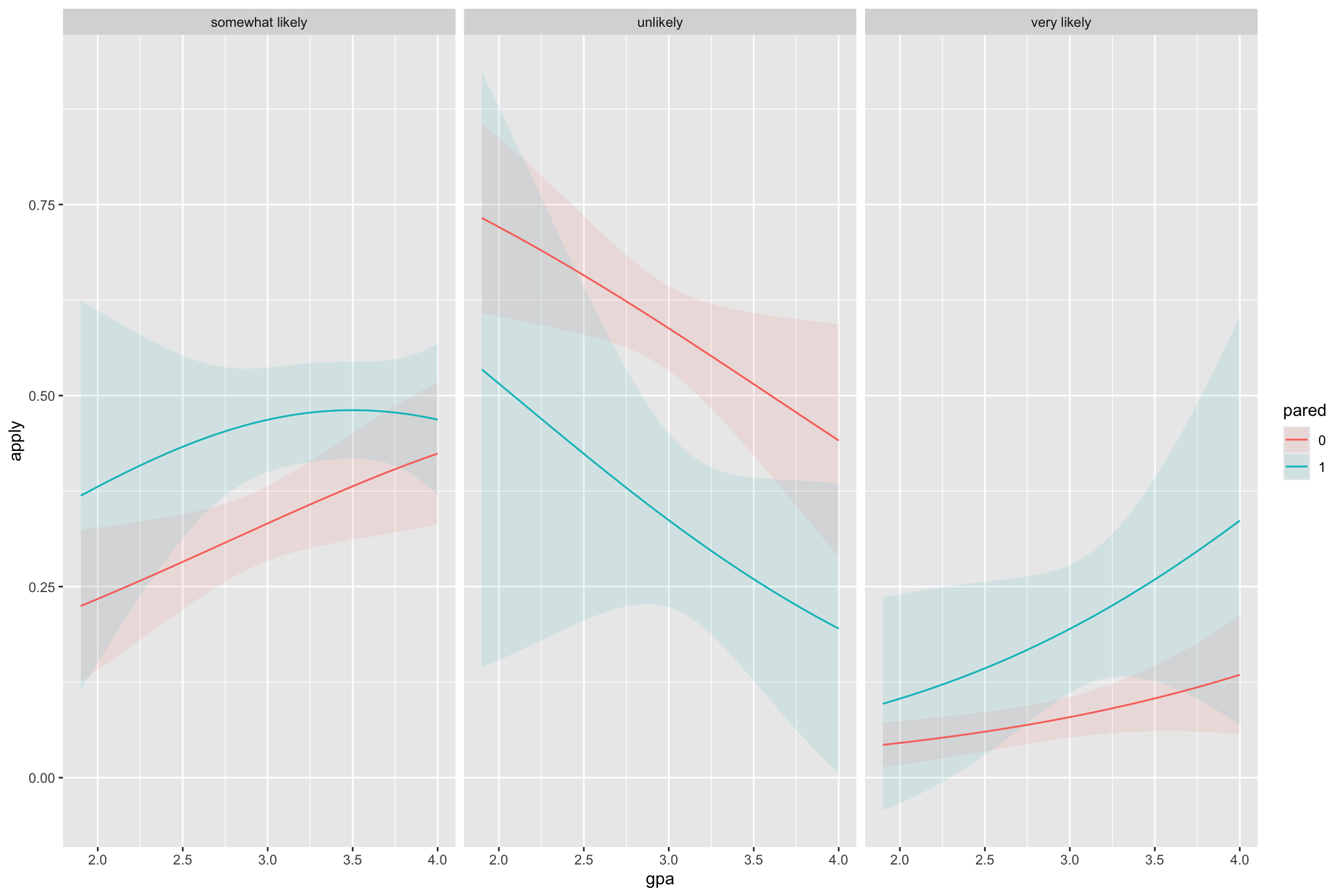
Pairwise comparisons

• Results are on the logit (latent scale) by default

Simple slopes

Latent scale

plot(effect("pared:gpa", ols3, latent = TRUE))

Marginal effects

avg_comparisons(ols3, terms="pared")

           Group   Term Contrast Estimate Std. Error      z Pr(>|z|)    S
 somewhat likely gpa       +1     0.08675     0.0376  2.307  0.02106  5.6
 somewhat likely pared     1 - 0  0.13017     0.0320  4.071  < 0.001 14.4
 somewhat likely public    1 - 0 -0.00916     0.0442 -0.207  0.83581  0.3
 unlikely        gpa       +1    -0.14264     0.0584 -2.441  0.01463  6.1
 unlikely        pared     1 - 0 -0.24714     0.0629 -3.928  < 0.001 13.5
 unlikely        public    1 - 0  0.01450     0.0694  0.209  0.83455  0.3
 very likely     gpa       +1     0.05589     0.0254  2.200  0.02782  5.2
 very likely     pared     1 - 0  0.11697     0.0385  3.034  0.00241  8.7
 very likely     public    1 - 0 -0.00534     0.0252 -0.212  0.83244  0.3
    2.5 %  97.5 %
  0.01305  0.1605
  0.06750  0.1928
 -0.09578  0.0775
 -0.25716 -0.0281
 -0.37047 -0.1238
 -0.12156  0.1506
  0.00609  0.1057
  0.04142  0.1925
 -0.05480  0.0441

Columns: term, group, contrast, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high 
Type:  prob 

Model fit

• Pseudo-\(R^2\)

library(easystats)
#model goodness
r2_mcfadden(ols2)

# R2 for Generalized Linear Regression
       R2: 0.033
  adj. R2: 0.030

Sample write-up

A proportional odds model was estimated to investigate factors (parent education, GPA, and public schooling) that influence whether undergraduates apply to graduate school (“unlikely,” “somewhat likely,” “very likely”). The overall model fit was poor, McFadden’s pseudo-R2 = .03. Parent education predicted the likelihood of applying to graduate school, b = 1.04, z = 3.942, p < .001, OR = 3.06. Students with parents that went to college increased the odds of applying to graduate school by about 206%. Whether parents went to public or private school did not affect whether students applied to graduate school, b = -0.06, z = -0.197, p = .844, OR = 0.94. GPA was also a significant predictor, b = 0.615, z = 2.363, p < .001, OR = 1.84. Each point increase on GPA was associated with a 84% increase in the likelihood of applying to college.

Multilevel ordinal regressions

• Repeated measures designs

• Clustered/nested designs

ols2_clmm = ordinal::clmm()